题目内容
(理)如图,已知四棱锥S—ABCD的底面是边长为4的正方形,S在底面上的射影O落在正方形ABCD内,且O到AB、AD的距离分别为2和1.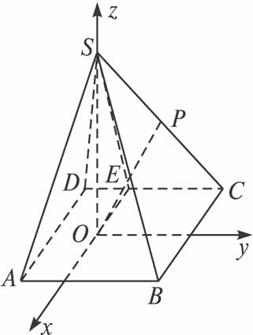
(1)求证:![]() 是定值.
是定值.
(2)已知P是SC的中点,且SO=3,问在棱SA上是否存在一点Q,使异面直线OP与BQ所成的角为90°?若存在,请给出证明,并求出AQ的长;若不存在,请说明理由.
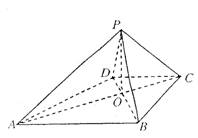
(文)如图,在四棱锥S—ABCD中,底面ABCD是正方形,SA⊥平面ABCD,且SA=AB,点E为AB的中点,点F为SC的中点.
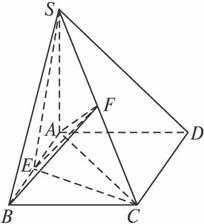
(1)求证:EF⊥CD;
(2)求证:平面SCD⊥平面SCE.
答案:(理)(1)证明:在△SDC内,作SE⊥CD交CD于E,连结OE.

∵SO⊥平面ABCD,∴SO⊥CD.∴CD⊥平面SOE.∴CD⊥OE.∴OE∥AD.∴DE=1,从而CE=3. ![]() =
=![]() cos∠SCD=
cos∠SCD=![]() =12,∴
=12,∴![]() 是定值.
是定值.
(2)解:以O为坐标原点,以OS所在直线为Oz轴,以过O且平行于AD的直线为Ox轴,以过O且平行于AB的直线为Oy轴,建立如图所示的空间直角坐标系.
于是,A(2,-1,0)、B(2,3,0)、C(-2,3,0)、S(0,0,3)、P(-1,![]() ,
,![]() ).
).
设点Q(x,y,z),则存在λ使![]() =λ
=λ![]() (这是关键!将点的坐标用一个变量表示),
(这是关键!将点的坐标用一个变量表示),
即(x-2,y+1,z)=λ(-2,1,3),
得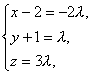 即
即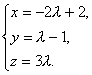
令![]() =(-1,
=(-1,![]() ,
,![]() )·(-2λ,λ-4,3λ)=8λ-6=0,得λ=
)·(-2λ,λ-4,3λ)=8λ-6=0,得λ=![]() .
.
由0<λ<1,知点Q在棱SA上,且Q(![]() ,-
,-![]() ,
,![]() ),|
),|![]() |=
|=![]() |
|![]() |=
|=![]() .
.
(文)证明:(1)如图,连结AC、AF、BF、EF,

∵SA⊥平面ABCD,∴AF为Rt△SAC斜边SC上的中线.∴AF=![]() SC.
SC.
又∵ABCD是正方形,∴CB⊥AB.而由SA⊥平面ABCD,得CB⊥SA.∴CB⊥平面SAB.∴CB⊥SB.∴BF为Rt△SBC斜边SC上的中线.∴BF=![]() SC.
SC.
∴△AFB为等腰三角形,EF⊥AB.又CD∥AB,∴EF⊥CD.
(2)由已知易得Rt△SAE≌Rt△CBE,∴SE=EC,即△SEC是等腰三角形.∴EF⊥SC.
又∵SC∩CD=C,∴EF⊥平面SCD.又EF![]() 平面SCE,∴平面SCD⊥平面SCE.
平面SCE,∴平面SCD⊥平面SCE.

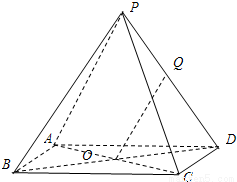
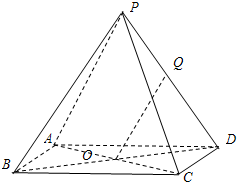 (2007•静安区一模)(理) 如图,已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,点O为该正方形的中心,侧棱PA=PC,PB=PD.
(2007•静安区一模)(理) 如图,已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,点O为该正方形的中心,侧棱PA=PC,PB=PD.
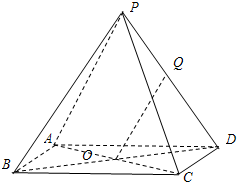 (理) 如图,已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,点O为该正方形的中心,侧棱PA=PC,PB=PD.
(理) 如图,已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,点O为该正方形的中心,侧棱PA=PC,PB=PD.