题目内容
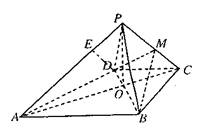
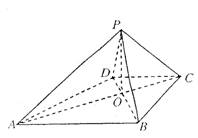
(08年滨州市质检三理) 如图,已知四棱锥P―ABCD的底面ABCD为等腰三角梯形,AB∥CD,AC⊥BC,AC∩BD=0,且顶点P在底面上的射影恰为O点,又OB=2,OP=![]() ,PD⊥PD.
,PD⊥PD.
(1)求二面角B―PA―D的余弦的绝对值;
(2)在棱PC上是否存在点M,使PC⊥平面BMD?若存在,求出点M的位置;若不存在,试说明理由。
(3)在(2)的条件下,求三棱锥C―BMD的体积.
解析:解法一:(I)![]()
![]() ∽
∽![]()
![]()
又∵四边形ABCD为等腰梯形
∴OC=OD=1,OA=OB=2
过点D作DE⊥PA于E,连结BE.
∵PO⊥面ABCD ∴PO⊥面ABCD
∵BD⊥AC ∴BD⊥面PAC. BD⊥PA
∴PA⊥面BDE. PA⊥BE
∴∠BED就是二面角B―PA―D的平面角
在△PAD中,PD=![]() ,
,![]()
在△PAB中,PA=![]()
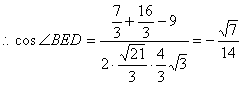
故二面角B―PA―D的余弦的绝对值为![]() .
.
(II)假设在棱PC上存在点M,使PC⊥面BMD.
由(I)知BD⊥PC.所以只需PC⊥OM即可
此时![]()
∴PM=2MC.
∴点M在PC的三等分点(靠近点C)处,可使PC⊥平面BMD.
(III)![]()
法二:顶点P在底面ABCD上的射影恰为O点
∴PO⊥BD,又PB⊥PD ∴Rt△POD∽Rt△BOP
∴![]()
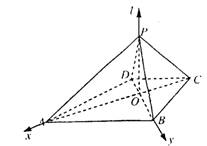
分别以直线OA、OB、OP为x轴、y轴、z轴
建立直角坐标系,
则A(2,0,0),B(0,2,0,),C(-1,0,0),
D(0,-1,0),P(0,0,![]() )
)
(I)![]()
![]()
设平面PAB,PAD的法向量分别为![]() 则
则

取![]()
![]()
∴二面角B―PA―D的余弦的绝对值是![]()
(II)设![]()
![]() ,
,![]() ,
,![]()
若PC⊥平面BMD,则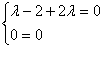
∴![]()
故点M在棱PC的三等分点(靠近点C)处,使PC⊥平面BMD.