题目内容
(本小题满分14分)已知圆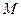 :
: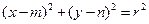 及定点
及定点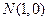 ,点
,点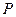 是圆
是圆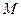 上的动点,点
上的动点,点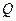 在
在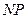 上,点
上,点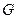 在
在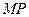 上,
上,
且满足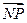 =2
=2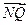 ,
,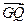 ·
·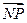 =
=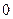 .
.
(1)若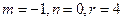 ,求点
,求点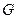 的轨迹
的轨迹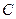 的方程;
的方程;
(2)若动圆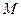 和(1)中所求轨迹
和(1)中所求轨迹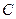 相交于不同两点
相交于不同两点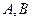 ,是否存在一组正实数
,是否存在一组正实数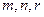 ,使得直线
,使得直线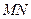 垂直平分线段
垂直平分线段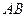 ,若存在,求出这组正实数;若不存在,说明理由.
,若存在,求出这组正实数;若不存在,说明理由.
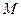 :
: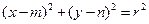 及定点
及定点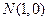 ,点
,点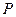 是圆
是圆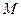 上的动点,点
上的动点,点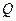 在
在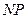 上,点
上,点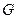 在
在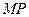 上,
上,且满足
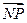 =2
=2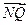 ,
,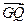 ·
·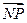 =
=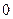 .
.(1)若
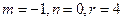 ,求点
,求点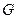 的轨迹
的轨迹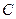 的方程;
的方程;(2)若动圆
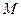 和(1)中所求轨迹
和(1)中所求轨迹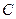 相交于不同两点
相交于不同两点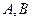 ,是否存在一组正实数
,是否存在一组正实数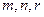 ,使得直线
,使得直线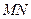 垂直平分线段
垂直平分线段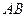 ,若存在,求出这组正实数;若不存在,说明理由.
,若存在,求出这组正实数;若不存在,说明理由.解:(1)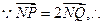
∴点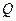 为
为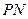 的中点,
的中点,
又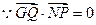 ,
,
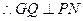 或
或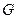 点与
点与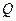 点重合.
点重合.
∴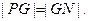 …………2分
…………2分
又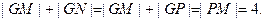
∴点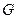 的轨迹是以
的轨迹是以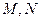 为焦点的椭圆,
为焦点的椭圆,
且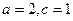 ,
,
∴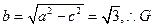
∴G的轨迹方程是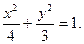 …………6分
…………6分
(2)解:不存在这样一组正实数,
下面证明: …………7分
由题意,若存在这样的一组正实数,
当直线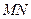 的斜率存在时,设之为
的斜率存在时,设之为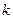 ,
,
故直线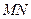 的方程为:
的方程为: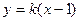 ,
,
设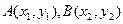 ,
,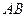 中点
中点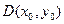 ,
,
则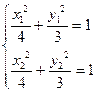 ,两式相减得:
,两式相减得:
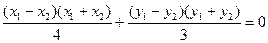 .…………9分
.…………9分
注意到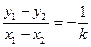 ,
,
且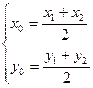 ,
,
则 , ②
, ②
又点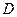 在直线
在直线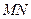 上,
上,
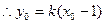 ,
,
代入②式得: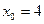 .
.
因为弦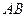 的中点
的中点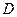 在⑴所给椭圆
在⑴所给椭圆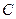 内,
内,
故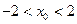 ,
,
这与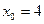 矛盾,
矛盾,
所以所求这组正实数不存在. …………13分
当直线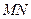 的斜率不存在时,
的斜率不存在时,
直线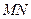 的方程为
的方程为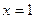 ,
,
则此时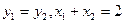 ,
,
代入①式得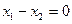 ,
,
这与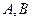 是不同两点矛盾.
是不同两点矛盾.
综上,所求的这组正实数不存在. …………14分
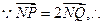
∴点
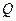 为
为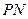 的中点,
的中点,又
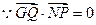 ,
,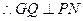 或
或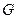 点与
点与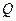 点重合.
点重合.∴
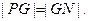 …………2分
…………2分又
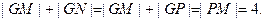
∴点
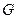 的轨迹是以
的轨迹是以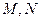 为焦点的椭圆,
为焦点的椭圆,且
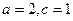 ,
,∴
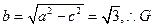
∴G的轨迹方程是
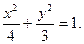 …………6分
…………6分(2)解:不存在这样一组正实数,
下面证明: …………7分
由题意,若存在这样的一组正实数,
当直线
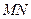 的斜率存在时,设之为
的斜率存在时,设之为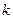 ,
,故直线
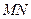 的方程为:
的方程为: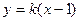 ,
,设
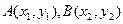 ,
,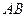 中点
中点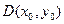 ,
,则
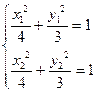 ,两式相减得:
,两式相减得: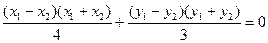 .…………9分
.…………9分注意到
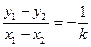 ,
,且
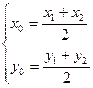 ,
,则
 , ②
, ②又点
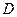 在直线
在直线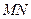 上,
上,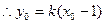 ,
,代入②式得:
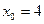 .
.因为弦
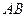 的中点
的中点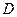 在⑴所给椭圆
在⑴所给椭圆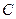 内,
内,故
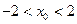 ,
,这与
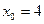 矛盾,
矛盾,所以所求这组正实数不存在. …………13分
当直线
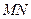 的斜率不存在时,
的斜率不存在时,直线
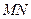 的方程为
的方程为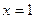 ,
,则此时
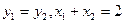 ,
,代入①式得
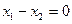 ,
,这与
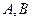 是不同两点矛盾.
是不同两点矛盾.综上,所求的这组正实数不存在. …………14分
略

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目



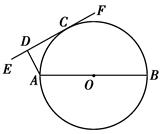
 1);
1);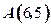 、
、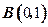 两点,并且圆心在直线
两点,并且圆心在直线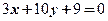 的圆的方程是 。
的圆的方程是 。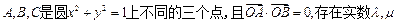 ,且
,且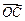 =
=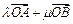
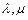 的关系为( )
的关系为( )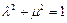
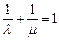
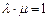
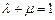
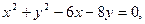 设该圆中过点(3,5)的最
设该圆中过点(3,5)的最 长弦和最短弦分别为AC和BD,则
长弦和最短弦分别为AC和BD,则