题目内容
（2013•长春一模）直线l1与l2相交于点A，动点B、C分别在直线l1与l2上且异于点A，若
与
的夹角为60°，|
|=2
，则△ABC的外接圆的面积为（ ）
| AB |
| AC |
| BC |
| 3 |
分析：先根据题意作图，从而得到∠BAC=60°，再根据正弦定理可求出△ABC的外接圆的半径，最后利用圆的面积公式解之即可．
解答：解：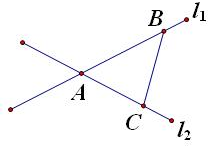
根据题意可知∠BAC=60°，|
|=2
，
根据正弦定理可知
=
=2R
∴R=2
则△ABC的外接圆的面积为π×22=4π
故选B．
根据题意可知∠BAC=60°，|| BC |
| 3 |
根据正弦定理可知
| BC |
| sin∠BAC |
2
| ||||
|
∴R=2
则△ABC的外接圆的面积为π×22=4π
故选B．
点评：本题主要考查了向量的夹角，以及正弦定理的应用和圆的面积的度量，同时考查了运算求解的能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目