题目内容

设y=f(x)是定义在［-1，1］上的函数，且满足:

(i)f(-1)=f(1)=0;

(ii)对任意的u、v∈［-1,1］都有|f(u)-f(v)|≤|u-v|.

(1)证明对x∈［-1,1］都有x-1≤f(x)≤1-x;

(2)证明对任意的u、v∈［-1,1］都有|f(u)-f(v)|≤1.

证明:(1)令u=x,v=1得

|f(x)-f(1)|≤|1-x|,

∵f(1)=0,∴|f(x)|≤1-x.

∴x-1≤f(x)≤1-x.

(2)当|u-v|≤1时,

|f(u)-f(v)|≤|u-v|≤1;

    当|u-v|＞1时,

    则u、v异号.不妨设u＜0,v＞0,

    则v-u＞1.

∴|f(u)-f(v)|=|f(u)-f(-1)+f(1)-f(v)|≤|f(u)-f(-1)|+|f(1)-f(v)|≤|u+1|+|1-v|=u+1+1-v=2-(v-u)＜1.

    综上,|f(u)-f(v)|≤1.

练习册系列答案
相关题目

设y=f(x)是定义在区间[－1，1]上的函数，且满足条件：①f(－1)=f(1)=0；②对任意的u，v∈[－1，1]，都有．

(1)证明：对任意的x∈[－1，1]，都有x－1≤f(x)≤1－x．

(2)证明：对任意的u，v∈[－1，1]，都有．

(3)在区间[－1，1]上是否存在满足题设条件的奇函数y=f(x)，且使得：

若存在，请举一例；若不存在，请说明理由．
设y=f(x)是定义在区间［-1,1］上的函数,且满足条件:

①f(-1)=f(1)=0;

②对任意u,v∈［-1,1］都有|f(u)-f(v)|≤|u-v|.

(1)证明对任意的x∈［-1,1］,都有x-1≤f(x)≤1-x;

(2)证明对任意的u,v∈［-1,1］,都有|f(u)-f(v)|≤1;

(3)在区间［-1,1］上是否存在满足条件的奇函数y=f(x),且使得

若存在,请举一例;若不存在,请说明理由.
设y=f(x)是定义在区间［-1,1］上的函数,且满足条件:

①f(-1)=f(1)=0;

②对任意u,v∈［-1,1］都有|f(u)-f(v)|≤|u-v|.

(1)证明对任意的x∈［-1,1］,都有x-1≤f(x)≤1-x;

(2)证明对任意的u,v∈［-1,1］,都有|f(u)-f(v)|≤1;

(3)在区间［-1,1］上是否存在满足条件的奇函数y=f(x),且使得

若存在,请举一例;若不存在,请说明理由.

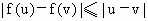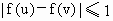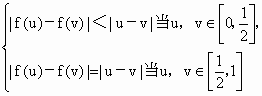
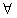设y=f(x)是定义在区间（a，b）（b＞a）上的函数，若对x1、x2∈（a，b），都有|f(x1)-f(x2)|≤|x1-x2|，则称y=f(x)是区间（a，b）上的平缓函数．
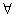（1）试证明对k∈R，f(x)=x2+kx+1都不是区间（-1，1）上的平缓函数；
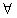（2）若f(x)是定义在实数集R上的、周期为T=2的平缓函数，试证明对x1、x2∈R，|f(x1)-f(x2)|≤1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网