题目内容
已知函数f(x)=ax+ -a(a∈R,a≠0)在x=3处的切线方程为(2a-1)x-2y+3=0
-a(a∈R,a≠0)在x=3处的切线方程为(2a-1)x-2y+3=0(1)若g(x)=f(x+1),求证:曲线g(x)上的任意一点处的切线与直线x=0和直线y=ax围成的三角形面积为定值;
(2)若f(3)=3,是否存在实数m,k,使得f(x)+f(m-x)=k对于定义域内的任意x都成立;
(3)若方程f(x)=t(x2-2x+3)|x|有三个解,求实数t的取值范围.
【答案】分析:(1)先求导数:f′(x)=a-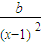 利用导数的几何意义求出切线方程,令x=0 得y=
利用导数的几何意义求出切线方程,令x=0 得y=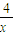 ; 再令y=ax得 x=2x,从而证得三角形面积为定值;
; 再令y=ax得 x=2x,从而证得三角形面积为定值;
(2)对于存在性问题,可先假设存在,即假设存在m,k满足题意,再利用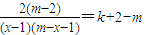 对定义域内任意x都成立,求出m,k,若出现矛盾,则说明假设不成立,即不存在;否则存在.
对定义域内任意x都成立,求出m,k,若出现矛盾,则说明假设不成立,即不存在;否则存在.
(3)由题意知,x-1+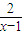 =t(x2-2x+3)|x|,分离出t:t=
=t(x2-2x+3)|x|,分离出t:t=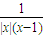 ,画出此函数的图象,由图可知t的取值范围.
,画出此函数的图象,由图可知t的取值范围.
解答:证明:(1)因为 f′(x)=a-
所以 f′(3)=a-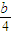 =
=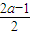 ,b=2…(2分)
,b=2…(2分)
又 g(x)=f(x+1)=ax+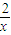 ,
,
设g(x)图象上任意一点P(x,y)因为 g′(x)=a-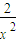 ,
,
所以切线方程为y-(ax+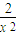 )=(a-
)=(a-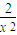 )(x-x)…(4分)
)(x-x)…(4分)
令x=0 得y=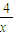 ; 再令y=ax得 x=2x,
; 再令y=ax得 x=2x,
故三角形面积S= |
|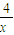 ||2x|=4,
||2x|=4,
即三角形面积为定值.…(6分)
解:(2)由f(3)=3得a=1,f(x)=x+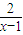 -1假设存在m,k满足题意,
-1假设存在m,k满足题意,
则有x-1+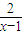 +m-x-1+
+m-x-1+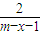 =k
=k
化简,得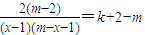 对定义域内任意x都成立,…(8分)
对定义域内任意x都成立,…(8分)
故只有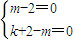 解得
解得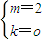
所以存在实数m=2,k=0使得f(x)+f(m-k)=k对定义域内的任意都成立.…(11分)
 (3)由题意知,x-1+
(3)由题意知,x-1+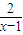 =t(x2-2x+3)|x|
=t(x2-2x+3)|x|
因为x≠0,且x≠1
化简,得 t=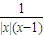 …(13分)
…(13分)
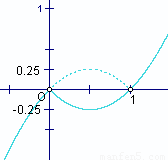
即 =|x|(x-1)…(15分)
=|x|(x-1)…(15分)
如图可知,- <
< <0
<0
所以t<-4即为t的取值范围.…(16分)
点评:本小题主要考查利用导数研究曲线上某点切线方程、利用导数研究函数的极值、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
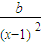 利用导数的几何意义求出切线方程,令x=0 得y=
利用导数的几何意义求出切线方程,令x=0 得y=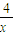 ; 再令y=ax得 x=2x,从而证得三角形面积为定值;
; 再令y=ax得 x=2x,从而证得三角形面积为定值;(2)对于存在性问题,可先假设存在,即假设存在m,k满足题意,再利用
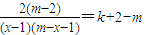 对定义域内任意x都成立,求出m,k,若出现矛盾,则说明假设不成立,即不存在;否则存在.
对定义域内任意x都成立,求出m,k,若出现矛盾,则说明假设不成立,即不存在;否则存在.(3)由题意知,x-1+
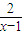 =t(x2-2x+3)|x|,分离出t:t=
=t(x2-2x+3)|x|,分离出t:t=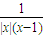 ,画出此函数的图象,由图可知t的取值范围.
,画出此函数的图象,由图可知t的取值范围.解答:证明:(1)因为 f′(x)=a-

所以 f′(3)=a-
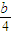 =
=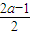 ,b=2…(2分)
,b=2…(2分)又 g(x)=f(x+1)=ax+
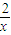 ,
,设g(x)图象上任意一点P(x,y)因为 g′(x)=a-
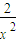 ,
,所以切线方程为y-(ax+
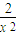 )=(a-
)=(a-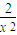 )(x-x)…(4分)
)(x-x)…(4分)令x=0 得y=
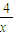 ; 再令y=ax得 x=2x,
; 再令y=ax得 x=2x,故三角形面积S=
 |
|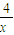 ||2x|=4,
||2x|=4,即三角形面积为定值.…(6分)
解:(2)由f(3)=3得a=1,f(x)=x+
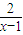 -1假设存在m,k满足题意,
-1假设存在m,k满足题意,则有x-1+
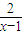 +m-x-1+
+m-x-1+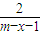 =k
=k化简,得
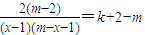 对定义域内任意x都成立,…(8分)
对定义域内任意x都成立,…(8分)故只有
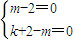 解得
解得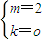
所以存在实数m=2,k=0使得f(x)+f(m-k)=k对定义域内的任意都成立.…(11分)
 (3)由题意知,x-1+
(3)由题意知,x-1+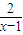 =t(x2-2x+3)|x|
=t(x2-2x+3)|x|因为x≠0,且x≠1
化简,得 t=
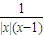 …(13分)
…(13分)即
 =|x|(x-1)…(15分)
=|x|(x-1)…(15分)如图可知,-
 <
< <0
<0所以t<-4即为t的取值范围.…(16分)
点评:本小题主要考查利用导数研究曲线上某点切线方程、利用导数研究函数的极值、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目