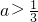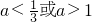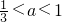Question

直线y=ax+2a-1，当-1≤x≤1时，y的值有正有负，则实数a的取值范围是（　　）

• A．a＞

  1

  3

• B．a＜

  1

  3

  或a＞1
• C．a＜1
• D．

  1

  3

  ＜a＜1

Answer 1

分析：根据y=ax+2a-1，当-1≤x≤1时，y的值有正有负，可以得到当x=-1，x=1时，函数值异号，因此得到（-a+2a-1）（a+2a-1）＜0，解此不等式即可求得实数a的取值范围．

解答：解：设f（x）=ax+2a-1，
∵当-1≤x≤1时，y的值有正有负
∴f（-1）f（1）＜0
∴（-a+2a-1）（a+2a-1）＜0，
解得

1

3

＜a＜1
故选D．

点评：本题考查函数零点的判定定理，考查解不等式，同时考查学生应用知识分析解决问题的能力，属于基础题．