题目内容
(2012•珠海二模)如图1,在边长为4cm的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于点B,构成一个三棱锥(如图2).
(1)判别MN与平面AEF的位置关系,并给予证明;
(2)证明:平面ABE⊥平面BEF;
(3)求多面体E-AFNM的体积.

(1)判别MN与平面AEF的位置关系,并给予证明;
(2)证明:平面ABE⊥平面BEF;
(3)求多面体E-AFNM的体积.
分析:(1)利用线线平行,即MN∥AF,利用线面平行的判定证明线面平行;
(2)利用线面垂直,证明面面垂直;
(3)利用体积比,即可求多面体E-AFNM的体积.
(2)利用线面垂直,证明面面垂直;
(3)利用体积比,即可求多面体E-AFNM的体积.
解答: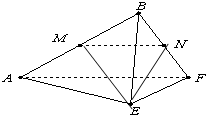 (1)解:MN∥平面AEF…(1分)
(1)解:MN∥平面AEF…(1分)
证明如下:因翻折后B、C、D重合,∴MN是△ABF的一条中位线,…(3分)
∴MN∥AF
又∵MN?平面AEF,AF?平面AEF
∴MN∥平面AEF.…(6分)
(2)证明:∵AB⊥BE,AB⊥BF,且BE∩BF=B
∴AB⊥平面BEF,…(8分)
而AB?平面ABE,∴平面ABE⊥平面BEF…(9分)
(3)解:∵AB=4,BE=BF=2,∴VA-BEF=
,…(11分)
又
=
=
…(13分)
∴VE-AFMN=2.…(14分).
 (1)解:MN∥平面AEF…(1分)
(1)解:MN∥平面AEF…(1分)证明如下:因翻折后B、C、D重合,∴MN是△ABF的一条中位线,…(3分)
∴MN∥AF
又∵MN?平面AEF,AF?平面AEF
∴MN∥平面AEF.…(6分)
(2)证明:∵AB⊥BE,AB⊥BF,且BE∩BF=B
∴AB⊥平面BEF,…(8分)
而AB?平面ABE,∴平面ABE⊥平面BEF…(9分)
(3)解:∵AB=4,BE=BF=2,∴VA-BEF=
| 8 |
| 3 |
又
| VE-AFNM |
| VE-ABF |
| SAFNM |
| S△ABF |
| 3 |
| 4 |
∴VE-AFMN=2.…(14分).
点评:本题考查线面平行,面面垂直,考查多面体体积的计算,掌握线面平行,面面垂直的判定方法是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目