题目内容
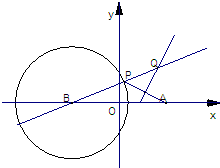
已知点A(5,0)和⊙B:(x+5)2+y2=36,P是⊙B上的动点,直线BP与线段AP的垂直平分线交于点Q.(1)证明点Q的轨迹是双曲线,并求出轨迹方程.
(2)若
 ,求点Q的坐标.
,求点Q的坐标.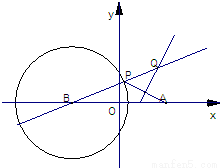
【答案】分析:(1)由点Q在线段AP的垂直平分线上,知|QP|=|QA|,所以||BQ|-|PQ||=||BQ|-|AQ||=6.由此能求出点Q的轨迹方程.
(2)以A、B、Q为三个顶点作平行四边形ABQC,则 .由
.由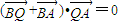 ,知
,知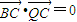 ,所以平行四边形ABQC是菱形,由此能求出点Q的坐标.
,所以平行四边形ABQC是菱形,由此能求出点Q的坐标.
解答:解:(1)∵点Q在线段AP的垂直平分线上,
∴|QP|=|QA|,
∴||BQ|-|PQ||=||BQ|-|AQ||=6.
∴点Q的轨迹是以A、B为焦点的双曲线.(4′)
其轨迹方程是 .(7′)
.(7′)
(2)以A、B、Q为三个顶点作平行四边形ABQC,
则 ∵
∵ ,
,
∴ ,
,
∴平行四边形ABQC是菱形,
∴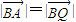 .(8′)
.(8′)
∴点Q在圆(x+5)2+y2=100上.
解方程组 .(10′)
.(10′)
得 或
或 .(12′)
.(12′)

点评:本题主要考查双曲线标准方程,简单几何性质,直线与双曲线的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.
(2)以A、B、Q为三个顶点作平行四边形ABQC,则
 .由
.由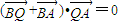 ,知
,知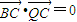 ,所以平行四边形ABQC是菱形,由此能求出点Q的坐标.
,所以平行四边形ABQC是菱形,由此能求出点Q的坐标.解答:解:(1)∵点Q在线段AP的垂直平分线上,
∴|QP|=|QA|,
∴||BQ|-|PQ||=||BQ|-|AQ||=6.
∴点Q的轨迹是以A、B为焦点的双曲线.(4′)
其轨迹方程是
 .(7′)
.(7′)(2)以A、B、Q为三个顶点作平行四边形ABQC,
则
 ∵
∵ ,
,∴
 ,
,∴平行四边形ABQC是菱形,
∴
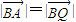 .(8′)
.(8′)∴点Q在圆(x+5)2+y2=100上.
解方程组
 .(10′)
.(10′)得
 或
或 .(12′)
.(12′)
点评:本题主要考查双曲线标准方程,简单几何性质,直线与双曲线的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2005•温州一模)已知点A(5,0)和⊙B:(x+5)2+y2=36,P是⊙B上的动点,直线BP与线段AP的垂直平分线交于点Q.
(2005•温州一模)已知点A(5,0)和⊙B:(x+5)2+y2=36,P是⊙B上的动点,直线BP与线段AP的垂直平分线交于点Q.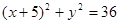 ,P是⊙B上的动点,直线BP与线段AP的垂直平分线交于点Q,则点Q(x,y)所满足的轨迹方程为(
▲ )
,P是⊙B上的动点,直线BP与线段AP的垂直平分线交于点Q,则点Q(x,y)所满足的轨迹方程为(
▲ )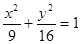 B.
B.  C .
C .  D.
D.