题目内容
若不等式组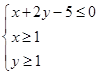 表示的平面区域是一个三角形,则此三角形的面积是_______;若
表示的平面区域是一个三角形,则此三角形的面积是_______;若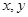 满足上述约束条件,则
满足上述约束条件,则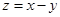 的最大值是
的最大值是
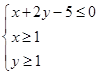 表示的平面区域是一个三角形,则此三角形的面积是_______;若
表示的平面区域是一个三角形,则此三角形的面积是_______;若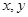 满足上述约束条件,则
满足上述约束条件,则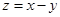 的最大值是
的最大值是 1, 2
分析:先根据约束条件画出可行域,然后求出区域的面积即可,设z=x-y,再利用z的几何意义求最值,只需求出直线z=x-y过可行域内的点A(3,1)时,从而得到z=x-y的最大值即可.

解:先画出约束条件
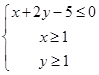 所表示的区域,如图.
所表示的区域,如图.所围成图形是一个三角形,其中:A (3,1),B(1,2),C(1,1).
∴三角形ABC的面积为S=
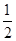 ×AC×BC=
×AC×BC=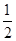 ×2×1=1;
×2×1=1;由图可知,当直线z=x-y过点A(3,1)时,z最大,
即最优解为A(3,1),
故Zmax=3-1=2.
故答案为:1,2.

练习册系列答案
相关题目
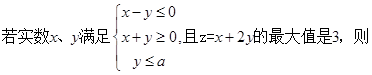
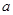 =( )
=( )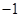
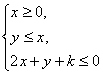 (k为常数)时,使z=x+3y的最大值为12的k值为
(k为常数)时,使z=x+3y的最大值为12的k值为 ,则
,则 的最大值是
的最大值是  满足条件
满足条件 若函数
若函数 的最大值为8,则
的最大值为8,则 的最小值为
的最小值为 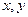 满足不等式组
满足不等式组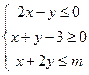 ,且
,且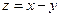 的最小值为
的最小值为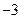 ,则实数
,则实数 的值是 ▲ .
的值是 ▲ .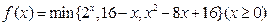 ,其中
,其中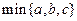 表示a,b,c三个数中的最小值,则
表示a,b,c三个数中的最小值,则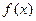 的最大值为( )
的最大值为( )
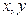 满足不等式组
满足不等式组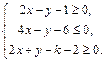 且
且 的最小值为
的最小值为 ,当
,当 时,实数
时,实数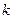 的取值范围是___________.
的取值范围是___________.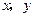 满足约束条件
满足约束条件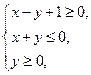 则目标函数
则目标函数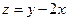 的最大值为
的最大值为