题目内容
本题设有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题做答,满分14分,如果多做,则按所做的前两题计分,做答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。
(1)(本小题满分7分)选修4-2:矩阵与变换
设矩阵![]() (其中a>0,b>0).
(其中a>0,b>0).
(I)若a=2,b=3,求矩阵M的逆矩阵M-1;
(II)若曲线C:x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C’:![]() ,求a,b的值.
,求a,b的值.
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在直接坐标系xOy中,直线l的方程为x-y+4=0,曲线C的参数方程为
 .
.
(I)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4,![]() ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(II)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
(3)(本小题满分7分)选修4-5:不等式选讲
设不等式![]() 的解集为M.
的解集为M.
(I)求集合M;
(II)若a,b∈M,试比较ab+1与a+b的大小.
(1)选修4—2:矩阵与变换
本小题主要考查矩阵与交换等基础知识,考查运算求解能力,考查化归与转化思想,满分7分。
解:(I)设矩阵M的逆矩阵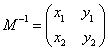 ,则
,则![]()
又![]() ,所以
,所以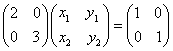 ,
,
所以![]()
故所求的逆矩阵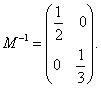
(II)设曲线C上任意一点![]() ,
,
它在矩阵M所对应的线性变换作用下得到点![]() ,
,
则![]()
![]()
又点![]() 在曲线
在曲线![]() 上,
上,
所以![]() ,,
,,
则![]() 为曲线C的方程,
为曲线C的方程,
又已知曲线C的方程为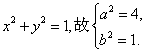
又![]()
(2)选修4—4:坐标系与参数方程
本小题主要考查极坐标与直角坐标的互化、椭圆的参数方程等基础知识,考查运算求解能力,考查化归与转化思想。满分7分。
解:(I)把极坐标系下的点![]() 化为直角坐标,得P(0,4)。
化为直角坐标,得P(0,4)。
因为点P的直角坐标(0,4)满足直线![]() 的方程
的方程![]() ,
,
所以点P在直线![]() 上,
上,
(II)因为点Q在曲线C上,故可设点Q的坐标为![]() ,
,
从而点Q到直线![]() 的距离为
的距离为
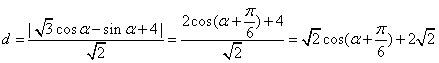 ,
,
由此得,当![]() 时,d取得最小值,且最小值为
时,d取得最小值,且最小值为![]()
(3)选修4—5:不等式选讲
本小题主要考查绝对值不等式等基础知识,考查运算求解能力,考查化归与转化思想,满分7分。
解:(I)由![]()
所以![]()
(II)由(I)和![]() ,
,
所以![]()
故![]()

 是将平面上每个点
是将平面上每个点 的横坐标乘
的横坐标乘 ,纵坐标乘
,纵坐标乘 ,变到点
,变到点 .
. 在变换
在变换 的极坐标方程为:
的极坐标方程为: ,直线
,直线 的参数方程为:
的参数方程为: (
( 为参数).
为参数). ,曲线
,曲线 的值.
的值. 为实数,且
为实数,且

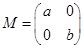 (其中a>0,b>0).
(其中a>0,b>0).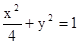 ,求a,b的值.
,求a,b的值. (其中a>0,b>0).
(其中a>0,b>0).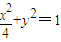 ,求a,b的值.
,求a,b的值. .
. ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;