题目内容
已知复数z1=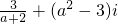 ,z2=2+(3a+1)i(a∈R,i是虚数单位).
,z2=2+(3a+1)i(a∈R,i是虚数单位).
(1)若复数z1-z2在复平面上对应点落在第一象限,求实数a的取值范围;
(2)若虚数z1是实系数一元二次方程x2-6x+m=0的根,求实数m值.
解:(1)由条件得,z1-z2=(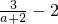 )+(a2-3a-4)i…(2分)
)+(a2-3a-4)i…(2分)
因为z1-z2在复平面上对应点落在第一象限,故有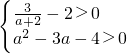 …(4分)
…(4分)
∴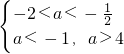 解得-2<a<-1…(6分)
解得-2<a<-1…(6分)
(2)因为虚数z1是实系数一元二次方程x2-6x+m=0的根
所以z1+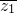 =
=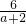 =6,即a=-1,…(8分)
=6,即a=-1,…(8分)
把a=-1代入,则z1=3-2i,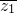 =3+2i,…(10分)
=3+2i,…(10分)
所以m=z1•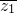 =13…(12分)
=13…(12分)
分析:(1)由题设条件,可先通过复数的运算求出的代数形式的表示,再由其几何意义得出实部与虚部的符号,转化出实数a所满足的不等式,解出其取值范围;
(2)实系数一元二次方程x2-6x+m=0的两个根互为共轭复数,利用根与系数的关系求出a的值,从而求出m的值.
点评:本题考查复数的代数形式及其几何意义,解题的关键是根据复数的代数形式的几何意义得出参数所满足的不等式,同时考查了运算求解的能力,属于基础题.
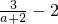 )+(a2-3a-4)i…(2分)
)+(a2-3a-4)i…(2分)因为z1-z2在复平面上对应点落在第一象限,故有
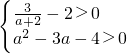 …(4分)
…(4分)∴
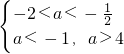 解得-2<a<-1…(6分)
解得-2<a<-1…(6分)(2)因为虚数z1是实系数一元二次方程x2-6x+m=0的根
所以z1+
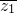 =
=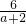 =6,即a=-1,…(8分)
=6,即a=-1,…(8分)把a=-1代入,则z1=3-2i,
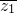 =3+2i,…(10分)
=3+2i,…(10分)所以m=z1•
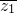 =13…(12分)
=13…(12分)分析:(1)由题设条件,可先通过复数的运算求出的代数形式的表示,再由其几何意义得出实部与虚部的符号,转化出实数a所满足的不等式,解出其取值范围;
(2)实系数一元二次方程x2-6x+m=0的两个根互为共轭复数,利用根与系数的关系求出a的值,从而求出m的值.
点评:本题考查复数的代数形式及其几何意义,解题的关键是根据复数的代数形式的几何意义得出参数所满足的不等式,同时考查了运算求解的能力,属于基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目