题目内容
若X是一个集合,集合v是一个以X的某些子集为元素的集合,且满足:
(1)X∈v,空集∅∈v;
(2)v中任意多个元素的并集属于v;
(3)v中任意多个元素的交集属于v;称v是集合X上的一个拓扑.
已知集合X={a,b,c},对于下列给出的四个集合v:
①v={∅,{a},{c},{a,b,c}};
②v={∅,{b},{c},{b,c},{a,b,c}};
③v={∅,{a},{a,b},{a,c}};
④v={∅,{a,c},{b,c},{c},{a,b,c}}.
则其中是集合X上的拓扑的集合v的序号是( )
(1)X∈v,空集∅∈v;
(2)v中任意多个元素的并集属于v;
(3)v中任意多个元素的交集属于v;称v是集合X上的一个拓扑.
已知集合X={a,b,c},对于下列给出的四个集合v:
①v={∅,{a},{c},{a,b,c}};
②v={∅,{b},{c},{b,c},{a,b,c}};
③v={∅,{a},{a,b},{a,c}};
④v={∅,{a,c},{b,c},{c},{a,b,c}}.
则其中是集合X上的拓扑的集合v的序号是( )
| A、①③ | B、③④ | C、①② | D、②④ |
考点:元素与集合关系的判断
专题:集合
分析:根据拓扑的定义,结合元素和集合的关系即可得到结论.
解答:解:利用拓扑的定义,可以发现集合X的空集和全集都属于它的拓扑v,∴③错误;
又∵v中任意多个元素的并集属于v,v中任意多个元素的交集属于v,∴①错误,
另外根据拓扑的定义可知②④正确,
故选:D.
又∵v中任意多个元素的并集属于v,v中任意多个元素的交集属于v,∴①错误,
另外根据拓扑的定义可知②④正确,
故选:D.
点评:本题主要考查元素和集合关系的判断,正确理解拓扑的定义是解决本题的关键.

练习册系列答案
相关题目
已知集合A={y|y=|x|-1,x∈R},B={x|x≥2},则下列结论正确的是( )
| A、-3∈A | B、3∉B | C、A∩B=B | D、A∪B=B |
设集合A={1,2,3},B={1,2,9},x∈A且x∉B,则x=( )
| A、1 | B、2 | C、3 | D、9 |
定义A×B={z|z=xy,x∈A且y∈B},若A={x|-1<x<2},B={-1,2},则A×B=( )
| A、{x|-1<x<2} | B、{-1,2} | C、{x|-2<x<2} | D、{x|-2<x<4} |
已知不等式{x|ax-2>0}的解集为{x|x<-4},则a的值为( )
A、
| ||
| B、2 | ||
C、-
| ||
| D、-2 |
 ,向量
,向量 .求向量
.求向量 ,使得
,使得 .
. (
( )任意排成
)任意排成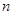 行
行 (
( )的比值
)的比值 ,称这些比值中的最小值为这个数表的“特征值”.若
,称这些比值中的最小值为这个数表的“特征值”.若 表示某个
表示某个 行第
行第 列的数(
列的数( ,
, ),且满足
),且满足 ,当
,当 时数表的“特征值”为_________
时数表的“特征值”为_________ (其中a>0,b>0).
(其中a>0,b>0). +y2=1,求a,b的值.
+y2=1,求a,b的值.