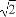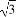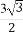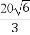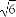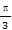题目内容
平面内给定三个向量a=(3,2),b=(-1,2),c=(4,1),回答下列问题:
(1)求3a+b-2c.
(2)求满足a=mb+nc的实数m,n.
(3)若(a+kc)∥(2b-a),求实数k.
(1) (0,6 (2) 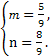 (3) k=-
(3) k=-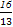 .
.
【解析】(1)3a+b-2c=3(3,2)+(-1,2)-2(4,1)=(9,6)+(-1,2)-(8,2)=(0,6).
(2)∵a=mb+nc,
∴(3,2)=m(-1,2)+n(4,1)=(-m+4n,2m+n).
∴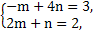 解得
解得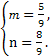
(3)∵(a+kc)∥(2b-a),
又a+kc=(3+4k,2+k),2b-a=(-5,2).
∴2×(3+4k)-(-5)×(2+k)=0,
∴k=-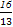 .
.

练习册系列答案
相关题目