题目内容
若等式sinx+siny=sin(x+y)成立,则必有
- A.x∈R,y∈R
- B.x=y=nπ,(n∈Z)
- C.x=-y
- D.x,y,x+y中,至少有一个为2nπ(n∈Z)
D
分析:先利用两角和公式对sin(y+x)展开,整理求得siny(1-cosx)+sinx(1-cosy)=0,进而可判断x,y,x+y中,至少有一个为2nπ(n∈Z).
解答:解法一:根据已知:sin(y+x)=sinycosx+cosysinx=siny+sinx
化简得:siny(1-cosx)+sinx(1-cosy)=0
即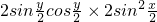 +
+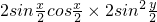 =0
=0
即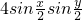 ×(
×(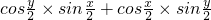 )=0
)=0
即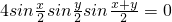
上式成立,所以必有 ,
, ,
, 中至少有一个为nπ(n∈Z)
中至少有一个为nπ(n∈Z)
即x,y,x+y中,至少有一个为2nπ(n∈Z)
故选D
解法二:排除法:ABC很容易找到反例
点评:本题主要考查了三角函数中的恒等变换应用.考查了学生演绎推理和创造性能力.
分析:先利用两角和公式对sin(y+x)展开,整理求得siny(1-cosx)+sinx(1-cosy)=0,进而可判断x,y,x+y中,至少有一个为2nπ(n∈Z).
解答:解法一:根据已知:sin(y+x)=sinycosx+cosysinx=siny+sinx
化简得:siny(1-cosx)+sinx(1-cosy)=0
即
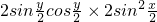 +
+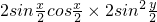 =0
=0即
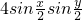 ×(
×(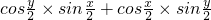 )=0
)=0即
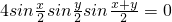
上式成立,所以必有
 ,
, ,
, 中至少有一个为nπ(n∈Z)
中至少有一个为nπ(n∈Z)即x,y,x+y中,至少有一个为2nπ(n∈Z)
故选D
解法二:排除法:ABC很容易找到反例
点评:本题主要考查了三角函数中的恒等变换应用.考查了学生演绎推理和创造性能力.

练习册系列答案
相关题目
若等式sinx+siny=sin(x+y)成立,则必有( )
| A、x∈R,y∈R | B、x=y=nπ,(n∈Z) | C、x=-y | D、x,y,x+y中,至少有一个为2nπ(n∈Z) |