题目内容
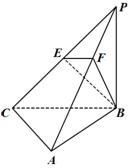
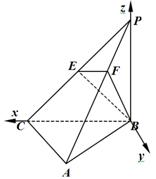
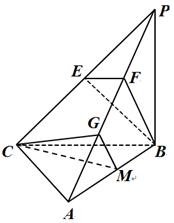
如图,三棱锥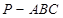 中,
中,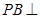 底面
底面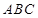 ,
,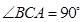 ,
,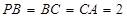 ,
,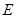 为
为 的中点,点
的中点,点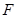 在
在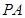 上,且
上,且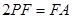 .
.
(1)求证:平面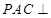 平面
平面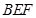 ;
;
(2)求平面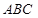 与平面
与平面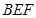 所成的二面角的平面角(锐角)的余弦值.
所成的二面角的平面角(锐角)的余弦值.
(1)证明:∵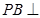 底面
底面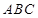 ,且
,且 底面
底面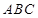 ,
,
∴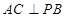 …………………1分
…………………1分
由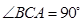 ,可得
,可得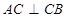 …………………………2分
…………………………2分
又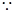
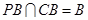 ,
,
∴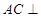 平面
平面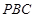 …………………………3分
…………………………3分
注意到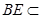 平面
平面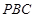 ,
,
∴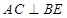 …………………………4分
…………………………4分
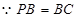 ,
,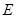 为
为 中点,
中点,
∴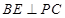 …………………………5分
…………………………5分
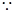
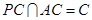 ,
, 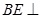 平面
平面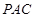 …………………………6分
…………………………6分
而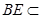 平面
平面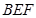 ,
,
∴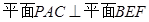 …………………………7分
…………………………7分
(2)方法一、如图,以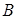 为原点、
为原点、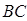 所在直线为
所在直线为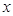 轴、
轴、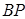 为
为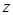 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则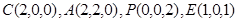 …………………………8分
…………………………8分
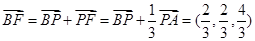 .
…………………………10分
.
…………………………10分
设平面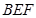 的法向量
的法向量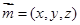 .
.
由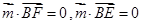 得
得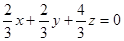 ,
,
即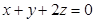 ……………(1)
……………(1)
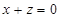 ……………(2)
……………(2)
取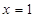 ,则
,则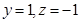 ,
,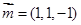 . …………………………12分
. …………………………12分
取平面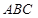 的法向量为
的法向量为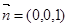
则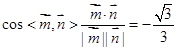 ,
,
故平面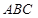 与平面
与平面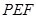 所成角的二面角(锐角)的余弦值为
所成角的二面角(锐角)的余弦值为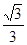 .
……………14分
.
……………14分
方法二、取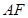 的中点
的中点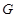 ,
,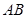 的中点
的中点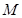 ,连接
,连接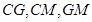 ,
,
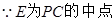 ,
,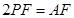 ,∴
,∴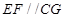 .
……………8分
.
……………8分
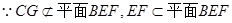 ,
,
∴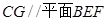 .
……………9分
.
……………9分
同理可证: .
又
.
又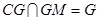 ,
,
∴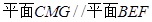 .…………10分
.…………10分
则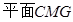 与平面
与平面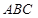 所成的二面角的平面角(锐角)就等于平面
所成的二面角的平面角(锐角)就等于平面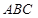 与平面
与平面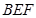 所成的二面角的平面角(锐角)
所成的二面角的平面角(锐角)
已知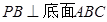 ,
,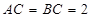 ,
,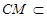 平面
平面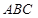
∴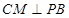 ,∴
,∴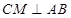 …………11分
…………11分
又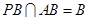 ,∴
,∴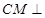 平面
平面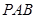
由于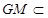 平面
平面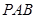 , ∴
, ∴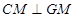
而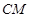 为
为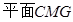 与平面
与平面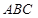 的交线,
的交线,
又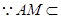 底面
底面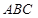 ,
,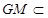 平面
平面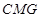
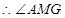 为二面角
为二面角
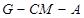 的平面角
…………12分
的平面角
…………12分
根据条件可得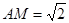 ,
,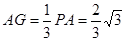
在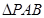 中,
中,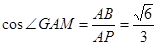
在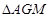 中,由余弦定理求得
中,由余弦定理求得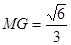 …………13分
…………13分
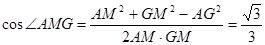
故平面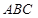 与平面
与平面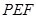 所成角的二面角(锐角)的余弦值为
所成角的二面角(锐角)的余弦值为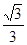 .
…………14分
.
…………14分
【解析】略

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 如图,三棱锥
如图,三棱锥
 中,
中, 底面
底面 ,
, ,
, ,
, 为
为 的中点,点
的中点,点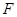 在
在 上,且
上,且 .
.
 平面
平面 ;
;  与平面
与平面 所成的二面角的平面角(锐角)的余弦值.
所成的二面角的平面角(锐角)的余弦值. 中,
中, ^底面
^底面 ,若底面
,若底面
 ,若
,若 是
是 的中点,
的中点,
 与
与 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).