题目内容
有四个关于三角函数的命题：
（1）?x∈R，sin2
+cos2=
；
（2）?x、y∈R，sin（x-y）=sinx-siny；
（3）?x∈[0，π]，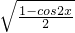
=sinx；
（4）sinx=cosy?x+y=
．
其中假命题的序号是 ________．
解：sin2+cos2=1，故（1）是假命题；
当x=y=0时，sin（x-y）=sinx-siny，故（2）成立；
?x∈[0，π]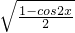，=sinx，（3）成立；
sinx=cosy?x+y=不成立，故（4）不成立．
故答案：（1）、（4）．
分析：由同角三角函数的关系知（1）是假命题；由三解函数的关系知（4）不成立．
点评：本题考查复合命题的真假，解题时要认真审题，仔细解答，注意公式的正确选用．
+cos2=1，故（1）是假命题；当x=y=0时，sin（x-y）=sinx-siny，故（2）成立；
?x∈[0，π]，
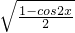=sinx，（3）成立；sinx=cosy?x+y=
不成立，故（4）不成立．故答案：（1）、（4）．
分析：由同角三角函数的关系知（1）是假命题；由三解函数的关系知（4）不成立．
点评：本题考查复合命题的真假，解题时要认真审题，仔细解答，注意公式的正确选用．
练习册系列答案
相关题目