题目内容
已知直线l:y=x+b及圆C:x2+y2=1,是否存在实数b,使自A(3,3)发出的光线被直线l反射后与圆相切于点( ,
, ),若存在,求出b的值;若不存在,试说明理由.
),若存在,求出b的值;若不存在,试说明理由.
【答案】分析:假设存在这样的实数b,则A(3,3)关于l的对称点A′为(3-b,3+b),故反射线所在直线方程为(25b+68)x+(15b-51)y-31b-51=0,又反射线与圆x2+y2=1相切,故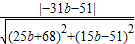 =1,由此能够推导出存在实数b=4满足条件.
=1,由此能够推导出存在实数b=4满足条件.
解答:解:假设存在这样的实数b,
则A(3,3)关于l的对称点A′为(3-b,3+b),
∴反射线所在直线方程为
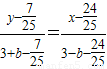 ,
,
即(25b+68)x+(15b-51)y-31b-51=0,
又反射线与圆x2+y2=1相切,
∴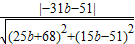 =1,
=1,
整理得:b2-8b+16=0,
∴b=4.
∴存在实数b=4满足条件.
点评:本题考查直线与圆的方程的综合运用,考查直线方程的求法和圆的基本性质,考查点到直线的距离公式.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
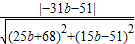 =1,由此能够推导出存在实数b=4满足条件.
=1,由此能够推导出存在实数b=4满足条件.解答:解:假设存在这样的实数b,
则A(3,3)关于l的对称点A′为(3-b,3+b),
∴反射线所在直线方程为
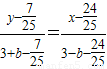 ,
,即(25b+68)x+(15b-51)y-31b-51=0,
又反射线与圆x2+y2=1相切,
∴
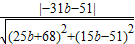 =1,
=1,整理得:b2-8b+16=0,
∴b=4.
∴存在实数b=4满足条件.
点评:本题考查直线与圆的方程的综合运用,考查直线方程的求法和圆的基本性质,考查点到直线的距离公式.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目