题目内容
5.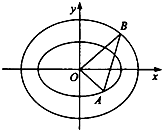 如图,在平面直角坐标系xOy中,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和
如图,在平面直角坐标系xOy中,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和C2:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1(m>n>0)上的动点,已知C1的焦距为2,点T在直线AB上,且
$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\overrightarrow{AB}$•$\overrightarrow{OT}$=0,又当动点A在x轴上的射影为C1的焦点时,点A恰在双曲线2y2-x2=1的渐近线上.
(Ⅰ)求椭圆C1的标准方程;
(Ⅱ)若C1与C2共焦点,且C1的长轴与C2的短轴长度相等,求|AB|2的取值范围;
(皿)若m,n是常数,且$\frac{1}{{m}^{2}}$-$\frac{1}{{n}^{2}}$=-$\frac{1}{2}$.证明|OT|为定值.
分析 (Ⅰ)求得双曲线的渐近线方程,结合条件可得A的坐标,再由椭圆的a,b,c的关系,可得椭圆方程;
(Ⅱ)结合条件,可得椭圆C2方程,设出OA,OB的方程,求得A,B的坐标,由$\overrightarrow{OA}•\overrightarrow{OB}$=0,运用勾股定理,可得AB的平方,结合基本不等式可得范围;
(Ⅲ)由T,A,B三点共线,$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\overrightarrow{AB}$•$\overrightarrow{OT}$=0,可得$\frac{1}{|OT{|}^{2}}$=$\frac{1}{|OA{|}^{2}}$+$\frac{1}{|OB{|}^{2}}$,将y=-$\frac{1}{k}$x代入椭圆$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1,求得B的坐标,化简整理可得|OT|定值.
解答 解:(Ⅰ)双曲线2y2-x2=1的渐近线方程为y=±$\frac{\sqrt{2}}{2}$x,
由题意可得椭圆C1的焦距2c=2,c=1,A(-1,-$\frac{\sqrt{2}}{2}$),
即有$\frac{{b}^{2}}{a}$=$\frac{\sqrt{2}}{2}$,a2-b2=1,解得a=$\sqrt{2}$,b=1,
即有椭圆C1的标准方程为$\frac{{x}^{2}}{2}$+y2=1;
(Ⅱ)C1的长轴与C2的短轴等长,即n=a=$\sqrt{2}$,
又C1,C2共焦点,可得m=$\sqrt{{n}^{2}+1}$=$\sqrt{3}$,
即有椭圆C2:$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1,
①当OA的斜率存在且不为0,将y=kx代入椭圆x2+2y2=2,
可得x2=$\frac{2}{1+2{k}^{2}}$,则|OA|2=$\frac{2(1+{k}^{2})}{1+2{k}^{2}}$=1+$\frac{1}{1+2{k}^{2}}$,
将y=-$\frac{1}{k}$x代入椭圆2x2+3y2=6,可得x2=$\frac{6{k}^{2}}{3+2{k}^{2}}$,
则|OB|2=$\frac{(1+{k}^{2})•6{k}^{2}}{{k}^{2}(3+2{k}^{2})}$=3-$\frac{3}{3+2{k}^{2}}$,
由$\overrightarrow{OA}•\overrightarrow{OB}$=0,可得|AB|2=|OA|2+|OB|2,
则|AB|2=4+$\frac{1}{1+2{k}^{2}}$-$\frac{3}{3+2{k}^{2}}$=4-$\frac{4{k}^{2}}{(1+2{k}^{2})(3+2{k}^{2})}$=4-$\frac{4}{8+4{k}^{2}+\frac{3}{{k}^{2}}}$<4,
又4k2+$\frac{3}{{k}^{2}}$≥4$\sqrt{3}$,当且仅当k2=$\frac{\sqrt{3}}{2}$时取得等号,
则有|AB|2≥4-$\frac{4}{8+4\sqrt{3}}$=2+$\sqrt{3}$,
即|AB|2∈[2+$\sqrt{3}$,4),
②当OA的斜率不存在或为0,有|AB|2=4,
综上可得,|AB|2的取值范围是[2+$\sqrt{3}$,4];
(Ⅲ)证明:由T,A,B三点共线,$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\overrightarrow{AB}$•$\overrightarrow{OT}$=0,
可得|OT|2=$\frac{|OA{|}^{2}•|OB{|}^{2}}{|AB{|}^{2}}$=$\frac{|OA{|}^{2}•|OB{|}^{2}}{|OA{|}^{2}+|OB{|}^{2}}$,
即有$\frac{1}{|OT{|}^{2}}$=$\frac{1}{|OA{|}^{2}}$+$\frac{1}{|OB{|}^{2}}$,
将y=-$\frac{1}{k}$x代入椭圆$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1,得x2=$\frac{1}{\frac{1}{{m}^{2}}+\frac{1}{{n}^{2}{k}^{2}}}$,
则|OB|2=$\frac{1+\frac{1}{{k}^{2}}}{\frac{1}{{m}^{2}}+\frac{1}{{n}^{2}{k}^{2}}}$=$\frac{1+{k}^{2}}{\frac{{k}^{2}}{{m}^{2}}+\frac{1}{{n}^{2}}}$,
则$\frac{1}{|OB{|}^{2}}$=$\frac{\frac{{k}^{2}}{{m}^{2}}+\frac{1}{{n}^{2}}}{1+{k}^{2}}$,又$\frac{1}{|OA{|}^{2}}$=$\frac{\frac{1}{2}+{k}^{2}}{1+{k}^{2}}$,
则有$\frac{1}{|OT{|}^{2}}$=$\frac{1}{|OA{|}^{2}}$+$\frac{1}{|OB{|}^{2}}$=$\frac{\frac{{k}^{2}}{{m}^{2}}+\frac{1}{{n}^{2}}}{1+{k}^{2}}$+$\frac{\frac{1}{2}+{k}^{2}}{1+{k}^{2}}$,
由于$\frac{1}{{m}^{2}}$-$\frac{1}{{n}^{2}}$=-$\frac{1}{2}$,
则$\frac{1}{|OT{|}^{2}}$=$\frac{(1+\frac{1}{{m}^{2}})(1+{k}^{2})}{1+{k}^{2}}$=1+$\frac{1}{{m}^{2}}$,即|OT|=$\frac{m}{\sqrt{1+{m}^{2}}}$,
容易验证当OA斜率不存在或为0,上述结论仍然成立,
综上可得|OT|为定值.
点评 本题考查椭圆的方程和性质,主要考查椭圆的方程的运用,联立直线方程,解方程,求交点,同时考查双曲线的渐近线方程和向量垂直的条件,以及基本不等式的运用,考查运算化简能力,属于难题.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案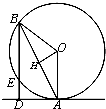 如图AB是圆O的一条弦,过点A作圆的切线AD,作BD⊥AD,与该圆交于点E,若AD=2$\sqrt{3}$,DE=2.
如图AB是圆O的一条弦,过点A作圆的切线AD,作BD⊥AD,与该圆交于点E,若AD=2$\sqrt{3}$,DE=2.