题目内容
(10分)已知函数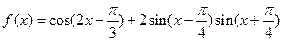
(Ⅰ)求函数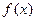 的最小正周期和图象的对称轴方程;
的最小正周期和图象的对称轴方程;
(Ⅱ)求函数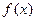 在区间
在区间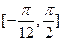 上的值域。
上的值域。
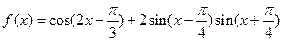
(Ⅰ)求函数
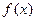 的最小正周期和图象的对称轴方程;
的最小正周期和图象的对称轴方程;(Ⅱ)求函数
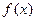 在区间
在区间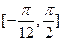 上的值域。
上的值域。解:(1)
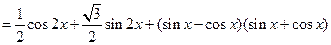


 ...3分
...3分
 ...4分
...4分
由
 函数图象的对称轴方程为
函数图象的对称轴方程为  ...5分
...5分
(2) ......6分
......6分
因为 在区间
在区间 上单调递增,
上单调递增,
在区间 上单调递减,......7分
上单调递减,......7分
所以 当 时,
时,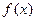 取最大值 1,又
取最大值 1,又  ,
,
当 时,
时,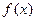 取最小值
取最小值 .......9分
.......9分
所以 函数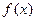 在区间
在区间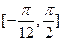 上的值域为
上的值域为 .......10分
.......10分

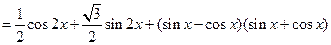


 ...3分
...3分 ...4分
...4分由

 函数图象的对称轴方程为
函数图象的对称轴方程为  ...5分
...5分(2)
 ......6分
......6分因为
 在区间
在区间 上单调递增,
上单调递增,在区间
 上单调递减,......7分
上单调递减,......7分所以 当
 时,
时,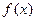 取最大值 1,又
取最大值 1,又  ,
,当
 时,
时,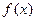 取最小值
取最小值 .......9分
.......9分所以 函数
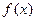 在区间
在区间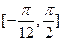 上的值域为
上的值域为 .......10分
.......10分略

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目


 ,
, ,
,
 时,求函数
时,求函数 的最大值;
的最大值; ,且
,且 在
在 的取值范围.
的取值范围. ,
, .设函数
.设函数 .
. 的最小正周期
的最小正周期 ,求函数
,求函数 (其中
(其中 )的图象如图所示,函数
)的图象如图所示,函数 ,
, 图像的对称轴方程;
图像的对称轴方程;
 时,求函数
时,求函数 的最大值和最小值及相应的
的最大值和最小值及相应的 的值;
的值; 在区间
在区间 上只有一个实数根,求实数
上只有一个实数根,求实数 的取值集合.
的取值集合.
 ·
· =
= ·
· 。
。 ,
, ,
, 成等差数列;
成等差数列; B及sinB+cosB的取值范围
B及sinB+cosB的取值范围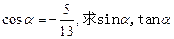 的值
的值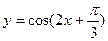 的图象的一个对称中心是( )
的图象的一个对称中心是( )



 图象是由函数
图象是由函数 的图象按如下变换所得
的图象按如下变换所得

 右移
右移