题目内容
已知中心在坐标原点,焦点在坐标轴上的椭圆G与x轴交于A、C两点,与y轴交于B、D两点,且A点的坐标为(-2,0),四边形ABCD的面积为4.
(1)求椭圆G的方程;
(2)过x轴上一点M(1,0)作一条不垂直于y轴的直线l,交椭圆G于E、F点,是否存在直线l,使得△AEF的面积为 ,说明理由.
,说明理由.
解:(1)∵A(-2,0),∴AC=4,
由题设知四边形ABCD为菱形,且其面积S=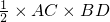 =4,
=4,
∴BD=2,
∴椭圆G是焦点在x轴上的椭圆,且a=2,b=1,
∴椭圆G的方程为 .
.
(2)∵直线l不垂直于y轴,∴设直线l的方程为x=my+1,
由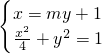 ,得(m2+4)y2+2my-3=0,
,得(m2+4)y2+2my-3=0,
△=4m2+12(m2+4)>0,
设E(x1,y1),F(x2,y2),则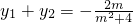 ,
,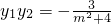 ,
,
x1+x2=m(y1+y2)+2=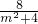 ,
,
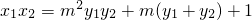 =
=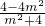 ,
,
设△AEF的面积为S,则S=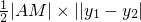 ,
,
故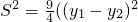 =
=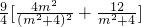
=9×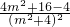
=9×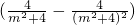 ,
,
令 ,则t
,则t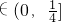 ,
,
则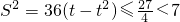 ,故S≠
,故S≠ ,
,
所以不存在直线l,使得△AEF的面积为 .
.
分析:(1)由A(-2,0),知AC=4,由题设知四边形ABCD为菱形,且其面积S=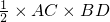 =4,故BD=2,所以椭圆G是焦点在x轴上的椭圆,且且a=2,b=1,由此能求出椭圆G的方程.
=4,故BD=2,所以椭圆G是焦点在x轴上的椭圆,且且a=2,b=1,由此能求出椭圆G的方程.
(2)设直线l的方程为x=my+1,由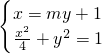 ,得(m2+4)y2+2my-3=0,△=4m2+12(m2+4)>0,设E(x1,y1),F(x2,y2),则
,得(m2+4)y2+2my-3=0,△=4m2+12(m2+4)>0,设E(x1,y1),F(x2,y2),则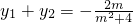 ,
,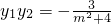 ,由此能推导出不存在直线l,使得△AEF的面积为
,由此能推导出不存在直线l,使得△AEF的面积为 .
.
点评:本题考查椭圆方程的求法和判断是否存在直线方程,使得三角形的面积为定值.综合性强,难度大,具有一定的探索性,对数学思维的要求较高,是高考的重点.解题时要认真审题,注意计算能力和解题能力的培养.
由题设知四边形ABCD为菱形,且其面积S=
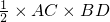 =4,
=4,∴BD=2,
∴椭圆G是焦点在x轴上的椭圆,且a=2,b=1,
∴椭圆G的方程为
 .
.(2)∵直线l不垂直于y轴,∴设直线l的方程为x=my+1,
由
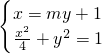 ,得(m2+4)y2+2my-3=0,
,得(m2+4)y2+2my-3=0,△=4m2+12(m2+4)>0,
设E(x1,y1),F(x2,y2),则
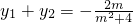 ,
,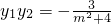 ,
,x1+x2=m(y1+y2)+2=
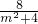 ,
,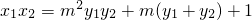 =
=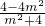 ,
,设△AEF的面积为S,则S=
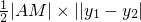 ,
,故
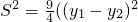 =
=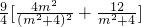
=9×
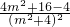
=9×
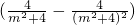 ,
,令
 ,则t
,则t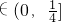 ,
,则
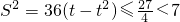 ,故S≠
,故S≠ ,
,所以不存在直线l,使得△AEF的面积为
 .
.分析:(1)由A(-2,0),知AC=4,由题设知四边形ABCD为菱形,且其面积S=
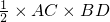 =4,故BD=2,所以椭圆G是焦点在x轴上的椭圆,且且a=2,b=1,由此能求出椭圆G的方程.
=4,故BD=2,所以椭圆G是焦点在x轴上的椭圆,且且a=2,b=1,由此能求出椭圆G的方程.(2)设直线l的方程为x=my+1,由
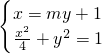 ,得(m2+4)y2+2my-3=0,△=4m2+12(m2+4)>0,设E(x1,y1),F(x2,y2),则
,得(m2+4)y2+2my-3=0,△=4m2+12(m2+4)>0,设E(x1,y1),F(x2,y2),则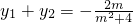 ,
,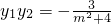 ,由此能推导出不存在直线l,使得△AEF的面积为
,由此能推导出不存在直线l,使得△AEF的面积为 .
.点评:本题考查椭圆方程的求法和判断是否存在直线方程,使得三角形的面积为定值.综合性强,难度大,具有一定的探索性,对数学思维的要求较高,是高考的重点.解题时要认真审题,注意计算能力和解题能力的培养.

练习册系列答案
相关题目
 (2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率
(2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率