题目内容
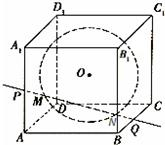 如图,在棱长为2的正方体ABCD-A1B1C1D1内有一个内切球O,则过棱AA1和BC的中点P、Q的直线与球面交点为M、N,则M、N两点间的球面距离为( )
如图,在棱长为2的正方体ABCD-A1B1C1D1内有一个内切球O,则过棱AA1和BC的中点P、Q的直线与球面交点为M、N,则M、N两点间的球面距离为( )A、
| ||||
B、
| ||||
C、arccos
| ||||
D、arccos(-
|
分析:欲求M、N两点间的球面距离,关键是求出球心角∠MON,故只须求出弦MN的长,也就是要求出球心到直线MN的距离即可,为了求出球心距,利用三角形POQ求解即可.
解答:解:易知△OPQ为等腰三角形,|OP|=|OQ|=
,
可求得O到PQ的距离为d=
=
,
PQ的直线被球面截在球内的线段的长为2
=
,
所以∠MON=
,
M、N两点间的球面距离为
.
故选B.
| 2 |
可求得O到PQ的距离为d=
(
|
| 1 | ||
|
PQ的直线被球面截在球内的线段的长为2
1-(
|
| 2 |
所以∠MON=
| π |
| 2 |
M、N两点间的球面距离为
| π |
| 2 |
故选B.
点评:本题主要考查了球面距离及相关计算,以及空间想象力,属于基础题.

练习册系列答案
相关题目
 如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )
如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )






