题目内容
【题目】已知曲线C的极坐标方程为ρ=![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数,0≤α<π).
(t为参数,0≤α<π).
(1)把曲线C的极坐标方程化为直角坐标方程,并说明曲线C的形状;
(2)若直线l经过点(1,0),求直线l被曲线C截得的线段AB的长.
【答案】(1)曲线C:y2=4x,顶点为O(0,0),焦点为F(1,0)的抛物线;(2)8
【解析】
(1)利用![]() 即可得出直角坐标方程;
即可得出直角坐标方程;
(2)直线l的参数方程![]() ( t为参数,0≤α<π).可得l经过点(0,1);若直线l经过点(1,0),得到
( t为参数,0≤α<π).可得l经过点(0,1);若直线l经过点(1,0),得到![]() ,得到直线l新的参数方程为
,得到直线l新的参数方程为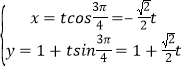 (t为参数).代入抛物线方程可得
(t为参数).代入抛物线方程可得![]() t+2=0,设A、B对应的参数分别为t1,t2,利用|AB|
t+2=0,设A、B对应的参数分别为t1,t2,利用|AB|![]() 即可得出.
即可得出.
(1)曲线C的极坐标方程ρ=![]() 化为ρ2sin2θ=4ρcosθ,
化为ρ2sin2θ=4ρcosθ,
得到曲线C的直角坐标方程为y2=4x,
故曲线C是顶点为O(0,0),焦点为F(1,0)的抛物线;
(2)直线l的参数方程为![]() ( t为参数,0≤α<π).
( t为参数,0≤α<π).
故l经过点(0,1);
若直线l经过点(1,0),则![]() ,
,
∴直线l的参数方程为 (t为参数).
(t为参数).
代入y2=4x,得![]() t+2=0
t+2=0
设A、B对应的参数分别为t1,t2,则t1+t2=﹣6![]() ,t1t2=2.
,t1t2=2.
|AB|=|t1﹣t2|=![]()
![]() =8.
=8.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目