题目内容
(10分) 设函数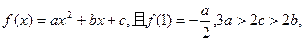 求证:
求证:
(1)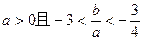 ;
;
(2)函数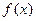 在区间(0,2)内至少有一个零点;
在区间(0,2)内至少有一个零点;
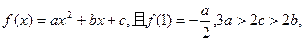 求证:
求证:(1)
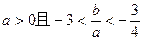 ;
; (2)函数
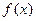 在区间(0,2)内至少有一个零点;
在区间(0,2)内至少有一个零点; 略
证明:(1)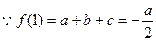

又

 ……………………2分
……………………2分
又2c=-3a-2b 由3a>2c>2b ∴3a>-3a-2b>2b
∵a>0 ………………………………………………4分
………………………………………………4分
(2)∵f(0)=c,f(2)=4a+2b+c=a-c………………………………6分
①当c>0时,∵ a>0,∴f(0)=c>0且
a>0,∴f(0)=c>0且
∴函数f(x)在区间(0,1 )内至少有一个零点……………………8分
)内至少有一个零点……………………8分
②当c≤0时,∵a>0

∴函数f(x)在区间(1,2)内至少有一个零点.
综合①②得f(x)在(0,2)内至少有一个零点…………………… ……10分
……10分
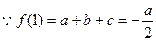

又


 ……………………2分
……………………2分又2c=-3a-2b 由3a>2c>2b ∴3a>-3a-2b>2b
∵a>0
 ………………………………………………4分
………………………………………………4分(2)∵f(0)=c,f(2)=4a+2b+c=a-c………………………………6分
①当c>0时,∵
 a>0,∴f(0)=c>0且
a>0,∴f(0)=c>0且
∴函数f(x)在区间(0,1
 )内至少有一个零点……………………8分
)内至少有一个零点……………………8分②当c≤0时,∵a>0


∴函数f(x)在区间(1,2)内至少有一个零点.
综合①②得f(x)在(0,2)内至少有一个零点……………………
 ……10分
……10分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
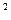 -1)x
-1)x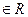 均成立,则实数的取值范围是
均成立,则实数的取值范围是  ,
, ,
, ,1)。
,1)。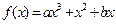 (其中常数a,b∈R),
(其中常数a,b∈R),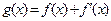 是奇函数.
是奇函数.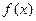 的表达式;(2)讨论
的表达式;(2)讨论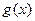 的单调性,并求
的单调性,并求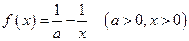
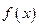 在上为增函数
在上为增函数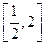 上的值域为
上的值域为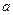 的值。
的值。 ),(m,y
),(m,y ),(m+1,y
),(m+1,y )都在二次函数y=x
)都在二次函数y=x -2x的图像上,
-2x的图像上,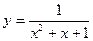 的最大值是 ( )
的最大值是 ( )



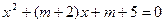 只有正根,则
只有正根,则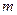 的取值范围是 ( ).
的取值范围是 ( ). 或
或



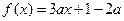 在
在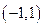 上存在
上存在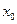 ,使得
,使得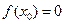 ,则
,则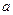 的取值范围( )
的取值范围( )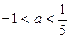 B
B 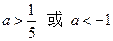 C
C 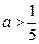 D
D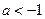
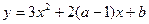 在区间
在区间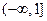 上为减函数,那么( )
上为减函数,那么( )


