题目内容
已知f(x)=2cos2x+ sin2x+a (a∈R , a为常数)
sin2x+a (a∈R , a为常数)
(Ⅰ) 若x∈R , 求f(x)的单调增区间;
(Ⅱ) 若x∈[0, ]时, f(x)的最大值为4, 并求此时f(x)的最小值。
]时, f(x)的最大值为4, 并求此时f(x)的最小值。
 sin2x+a (a∈R , a为常数)
sin2x+a (a∈R , a为常数)(Ⅰ) 若x∈R , 求f(x)的单调增区间;
(Ⅱ) 若x∈[0,
 ]时, f(x)的最大值为4, 并求此时f(x)的最小值。
]时, f(x)的最大值为4, 并求此时f(x)的最小值。[kπ- , kπ+
, kπ+ ] k∈Z.
] k∈Z.
】f(x)min=2 (
( )+ 1+1=1
)+ 1+1=1
 , kπ+
, kπ+ ] k∈Z.
] k∈Z.】f(x)min=2
 (
( )+ 1+1=1
)+ 1+1=1解: (Ⅰ)f(x)=2cos2x+ sin2x+a
sin2x+a
= cos2x+ sin2x+ a+1
sin2x+ a+1
="2" sin(2x+ ) +a+1,
) +a+1,
∴f(x)的单调增 区间为[kπ-
区间为[kπ- , kπ+
, kπ+ ] k∈Z. ………6分
] k∈Z. ………6分
(Ⅱ) ∵x∈[0, ]时, f(x)的最大值为4,
]时, f(x)的最大值为4,
∴ ≤2x+
≤2x+ ≤
≤ .
.
f(x)max="2+" a+1=4,
∴a="1." ………………………………………9分
故:当2x+ =
= ,即
,即 时,
时,
f(x)min=2 (
( )+ 1+1=1…………………………12分
)+ 1+1=1…………………………12分
 sin2x+a
sin2x+a= cos2x+
 sin2x+ a+1
sin2x+ a+1="2" sin(2x+
 ) +a+1,
) +a+1, ∴f(x)的单调增
 区间为[kπ-
区间为[kπ- , kπ+
, kπ+ ] k∈Z. ………6分
] k∈Z. ………6分(Ⅱ) ∵x∈[0,
 ]时, f(x)的最大值为4,
]时, f(x)的最大值为4, ∴
 ≤2x+
≤2x+ ≤
≤ .
. f(x)max="2+" a+1=4,
∴a="1." ………………………………………9分
故:当2x+
 =
= ,即
,即 时,
时,f(x)min=2
 (
( )+ 1+1=1…………………………12分
)+ 1+1=1…………………………12分
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
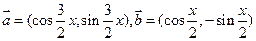 若
若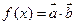 .
. 的最小正周期;
的最小正周期; 求函数
求函数 的最大值为2。
的最大值为2。 的值及
的值及 的最小正周期;
的最小正周期;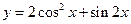 的最小值是__________
的最小值是__________ 的最小正周期为___________
的最小正周期为___________ 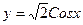 的图象,只需将函数
的图象,只需将函数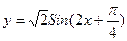 的图象上所有的点作( )
的图象上所有的点作( )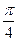 个单位长度;
个单位长度;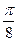 个单位长度;
个单位长度;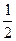 倍,再向右平行移动
倍,再向右平行移动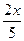 +cos
+cos ;③函数f(x)的图象上相邻的两条对称轴之间的距离是
;③函数f(x)的图象上相邻的两条对称轴之间的距离是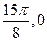 )是函数f(x)图象的一个对称中心.
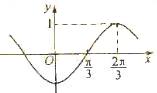
)是函数f(x)图象的一个对称中心.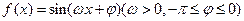 的图象如图所示,则
的图象如图所示,则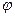 = ▲
= ▲ 
 ,下列判断正确的是
,下列判断正确的是

 ,周期是
,周期是