题目内容
16.已知函数f(x)=$\left\{\begin{array}{l}{2,x≥0}\\{-x+2,x<0}\end{array}\right.$,则满足不等式f(3-x2)<f(2x)的x的取值范围为(-3,0).分析 直接画出函数的图象,利用函数的单调性,转化不等式为代数形式的不等式,求出结果即可.
解答 解:作出f(x)图象如图: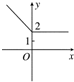
∵f(3-x2)<f(2x),
∴$\left\{\begin{array}{l}3-{x}^{2}>2x\\ 2x<0\end{array}\right.$,解得-3<x<0.
故答案为:(-3,0).
点评 本题考查函数的图象的应用,函数的单调性以及转化思想的求法,考查计算能力.

练习册系列答案
相关题目