题目内容

（14分）
设集合W由满足下列两个条件的数列构成：
①
②存在实数M，使（n为正整数）
（I）在只有5项的有限数列
；试判断数列是否为集合W的元素；
（II）设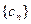是等差数列，是其前n项和，证明数列；并写出M的取值范围；
（III）设数列且对满足条件的常数M，存在正整数k，使
求证：

（I）对于数列，当n=1时，
显然不满足集合W的条件，①
故不是集合W中的元素，                          …………2分
对于数列，当时，
不仅有
而且有，
显然满足集合W的条件①②，
故是集合W中的元素.                              …………4分
（II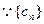）是等差数列，是其前n项和，
设其公差为d，


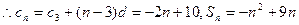          …………7分



的最大值是
即
，且M的取值范围是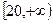                 …………9分
（III）证明：
整理，

又
                                  …………14分

解析

练习册系列答案
相关题目
精英家教网设集合W由满足下列两个条件的数列{an}构成：
①
an+an+22
＜an+1；②存在实数M，使an≤M．（ n为正整数）
（Ⅰ）在只有5项的有限数列{an}、{bn}中，其中a1=1，a2=2，a3=3，a4=4，a5=5；b1=1，b2=4，b3=5，b4=4，b5=1，试判断数列{an}、{bn}是否为集合W中的元素；
（Ⅱ）设{cn}是等差数列，Sn是其前n项和，c3=4，S3=18，证明数列{Sn}∈W；并写出M的取值范围；
（Ⅲ）设数列{dn}∈W，且对满足条件的常数M，存在正整数k，使dk=M．
求证：dk+1＞dk+2＞dk+3．
设集合W由满足下列两个条件的数列{an}构成：①
an+an+2
2
＜an+1；②存在实数M，使an≤M．（n为正整数）
（Ⅰ）在只有5项的有限数列{an}、{bn}中，其中a1=1，a2=2，a3=3，a4=4，a5=5；b1=1，b2=4，b3=5，b4=4，b5=1；试判断数列{an}、{bn}是否为集合W中的元素；
（Ⅱ）设{cn}是各项为正数的等比数列，Sn是其前n项和，c3=
1
4
，S3=
7
4
，试证明{Sn}∈W，并写出M的取值范围；
（Ⅲ）设数列{dn}∈W，对于满足条件的M的最小值M0，都有dn≠M0（n∈N*）．求证：数列{dn}单调递增．
（2012•房山区一模）设集合W由满足下列两个条件的数列{an}构成：
①
an+an+2
2
＜an+1；②存在实数M，使an≤M．（n为正整数）．在以下数列
（1）{n2+1}；  （2）{
2n+9
2n+11
}；  （3）{2+
4
n
}；  （4）{1-
1
2n
}
中属于集合W的数列编号为（　　）

（14分）设集合W由满足下列两个条件的数列构成：
①
②存在实数M，使（n为正整数）
（I）在只有5项的有限数列
；试判断数列是否为集合W的元素；
（II）设是各项为正的等比数列，是其前n项和，证明数列；并写出M的取值范围；
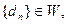（III）设数列且对满足条件的M的最小值M0，都有.
求证：数列单调递增.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网