题目内容
 设集合W由满足下列两个条件的数列{an}构成:
设集合W由满足下列两个条件的数列{an}构成:①
| an+an+2 | 2 |
(Ⅰ)在只有5项的有限数列{an}、{bn}中,其中a1=1,a2=2,a3=3,a4=4,a5=5;b1=1,b2=4,b3=5,b4=4,b5=1,试判断数列{an}、{bn}是否为集合W中的元素;
(Ⅱ)设{cn}是等差数列,Sn是其前n项和,c3=4,S3=18,证明数列{Sn}∈W;并写出M的取值范围;
(Ⅲ)设数列{dn}∈W,且对满足条件的常数M,存在正整数k,使dk=M.
求证:dk+1>dk+2>dk+3.
分析:(Ⅰ)要判断数列不为集合中的元素,只需要在数列中找一个元素不是集合中的元素即可.要判断数列为集合中的元素,需要严格证明,对于数列{bn},当n?{1,2,3,4,5}时,看数列{bn}是否满足集合W的条件①②即可.
(Ⅱ)是证明题.要证明数列{Sn}∈W,首先利用题中的条件:{cn}是等差数列,Sn是其前n项和,c3=4,S3=18确定出数列{Sn},然后再证明满足①②即可.
(Ⅲ)也是证明题.要求证dk+1>dk+2>dk+3,数列{dn}∈W所以满足W的两个条件,得到
<dk+1.整理得dk+2<dk+1+(dk+1-dk)=dk+1+(dk+1-M),因为dk=M,得到dk+1≤M,即dk+2<dk+1;又因为
<dk+2,得到dk+3<dk+2+(dk+2-dk+1)<dk+2,整理可得证.
(Ⅱ)是证明题.要证明数列{Sn}∈W,首先利用题中的条件:{cn}是等差数列,Sn是其前n项和,c3=4,S3=18确定出数列{Sn},然后再证明满足①②即可.
(Ⅲ)也是证明题.要求证dk+1>dk+2>dk+3,数列{dn}∈W所以满足W的两个条件,得到
| dk+dk+2 |
| 2 |
| dk+1+dk+3 |
| 2 |
解答:解:(Ⅰ)对于数列{an},当n=1时,
=2=a2,
显然不满足集合W的条件①,故{an}不是集合W中的元素.(2分)
对于数列{bn},当n={1,2,3,4,5}时,
不仅有
=3<b2,
=4<b3,
=3<b4,
而且有bn≤5,显然满足集合W的条件①②,故{bn}是集合W中的元素.(4分)
(Ⅱ)∵{cn}是等差数列,Sn是其前n项和,c3=4,S3=18,设其公差为d,
∴c3-2d+c3-d+c3=18,
∴d=-2
∴cn=c3+(n-3)d=-2n+10,Sn=-n2+9n(7分)
∵
-Sn+1=-1<0,∴
<Sn+1;
∵Sn=-(n-
)2+
,∴Sn的最大值是S4=S5=20,即Sn≤S4=20.
∴{Sn}∈W,且M的取值范围是[20,+∞)(9分)
(Ⅲ)证明:∵{dn}∈W,∴
<dk+1,
整理dk+2<dk+1+(dk+1-dk)=dk+1+(dk+1-M),
∵dk=M,∴dk+1≤M,∴dk+2<dk+1;
又∵
<dk+2,∴dk+3<dk+2+(dk+2-dk+1)<dk+2,
∴dk+1>dk+2>dk+3.(14分)
| a1+a3 |
| 2 |
显然不满足集合W的条件①,故{an}不是集合W中的元素.(2分)
对于数列{bn},当n={1,2,3,4,5}时,
不仅有
| b1+b3 |
| 2 |
| b2+b4 |
| 2 |
| b3+b5 |
| 2 |
而且有bn≤5,显然满足集合W的条件①②,故{bn}是集合W中的元素.(4分)
(Ⅱ)∵{cn}是等差数列,Sn是其前n项和,c3=4,S3=18,设其公差为d,
∴c3-2d+c3-d+c3=18,
∴d=-2
∴cn=c3+(n-3)d=-2n+10,Sn=-n2+9n(7分)
∵
| Sn+Sn+2 |
| 2 |
| Sn+Sn+2 |
| 2 |
∵Sn=-(n-
| 9 |
| 2 |
| 81 |
| 4 |
∴{Sn}∈W,且M的取值范围是[20,+∞)(9分)
(Ⅲ)证明:∵{dn}∈W,∴
| dk+dk+2 |
| 2 |
整理dk+2<dk+1+(dk+1-dk)=dk+1+(dk+1-M),
∵dk=M,∴dk+1≤M,∴dk+2<dk+1;
又∵
| dk+1+dk+3 |
| 2 |
∴dk+1>dk+2>dk+3.(14分)
点评:此题考查运用题中定义的函数解决问题的能力,以及数列与集合关系的判断.

练习册系列答案
相关题目
 构成:
构成:
 (n为正整数)
(n为正整数)
 ;试判断数列
;试判断数列 是否为集合W的元素;
是否为集合W的元素; 是各项为正的等比数列,
是各项为正的等比数列, 是其前n项和,
是其前n项和, 证明数列
证明数列 ;并写出M的取值范围;
;并写出M的取值范围;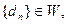 且对满足条件的M的最小值M0,都有
且对满足条件的M的最小值M0,都有 .
. 单调递增.
单调递增. 构成:
构成:
 (n为正整数)
(n为正整数)
 ;试判断数列
;试判断数列 是否为集合W的元素;
是否为集合W的元素;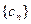 是等差数列,
是等差数列, 是其前n项和,
是其前n项和, 证明数列
证明数列 ;并写出M的取值范围;
;并写出M的取值范围; 且对满足条件的常数M,存在正整数k,使
且对满足条件的常数M,存在正整数k,使
