题目内容
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),以原点
),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 与
与![]() 的直角坐标方程;
的直角坐标方程;
(2)当![]() 与
与![]() 有两个公共点时,求实数
有两个公共点时,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (
(![]() ,
, ![]() ),
),![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据诱导公式平方和为1消去参数![]() ,可得曲线
,可得曲线![]() 的普通方程,根据
的普通方程,根据![]() 可求出曲线
可求出曲线![]() 的直角坐标方程;(2)先求出曲线
的直角坐标方程;(2)先求出曲线![]() 的轨迹,再根据图象找出
的轨迹,再根据图象找出![]() 与
与![]() 有两个公共点时的临界情况,求出参数的范围即可.
有两个公共点时的临界情况,求出参数的范围即可.
试题解析:
(1)∵曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),
),
∴曲线![]() 的普通方程为:
的普通方程为: ![]() (
(![]() ,
, ![]() ),
),
∵曲线![]() 的极坐标方程为
的极坐标方程为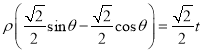 ,
,
∴曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)∵曲线![]() 的普通方程为:
的普通方程为: ![]() (
(![]() ,
, ![]() )为半圆弧,由曲线
)为半圆弧,由曲线![]() 于
于![]() 有两个公共点,则当
有两个公共点,则当![]() 与
与![]() 相切时,得
相切时,得![]() ,整理得
,整理得![]() ,
,
∴![]() 或
或![]() (舍去),
(舍去),
当![]() 过点
过点![]() 时,
时, ![]() ,所以t=-1.
,所以t=-1.
∴当![]() 与
与![]() 有两个公共点时,
有两个公共点时, ![]() .
.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
(1)请将上表数据补充完整;函数![]() 的解析式为
的解析式为![]() (直接写出结果即可);
(直接写出结果即可);
(2)根据表格中的数据作出![]() 一个周期的图象;
一个周期的图象;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.