题目内容
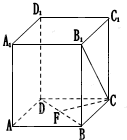 在棱长为2的正方体ABCD-A1B1C1D1中,已知F是线段BD的中点.
在棱长为2的正方体ABCD-A1B1C1D1中,已知F是线段BD的中点.(Ⅰ)试在棱D1D上确定一点E,使得EF⊥B1C;
(Ⅱ)在(Ⅰ)的条件下,求三棱锥B1-EFC的体积.
分析:(1)当点E为棱DD1的中点时,会使得EF⊥B1C,下面用下面垂直来证明即可;
(2)先由已知结合(1)得出垂直关系,再由几何关系求出三棱锥的底面和高,代公式可求.
(2)先由已知结合(1)得出垂直关系,再由几何关系求出三棱锥的底面和高,代公式可求.
解答: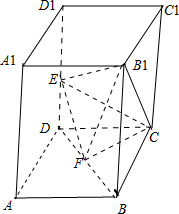 解:(1)当点E为棱DD1的中点时,会使得EF⊥B1C.下面证明:…(2分)
解:(1)当点E为棱DD1的中点时,会使得EF⊥B1C.下面证明:…(2分)
∵E、F分别为棱DD1、BD的中点,∴EF∥BD1,…(3分)
∵B1C⊥BC1,B1C⊥C1D1,又BC1∩C1D1=C1,∴B1C⊥平面BC1D1,∴B1C⊥BD1
同理可得B1C⊥BD,又BD∩BD1=B,
故BD1⊥平面AB1C,所以B1C⊥BD1…(5分)
即EF⊥B1C;…(6分)
(2)由(1)可知:EF⊥B1C,又EF⊥FC,故EF⊥平面B1CF,
又EF=
BD1=
.…(7分)
CF=
,B1C=2
,B1F=
,满足勾股定理…(8分)
故S△B1CF=
×
×
=
.…(10分)
故三棱锥B1-EFC的体积为V=
×
×
=1.…(13分)
 解:(1)当点E为棱DD1的中点时,会使得EF⊥B1C.下面证明:…(2分)
解:(1)当点E为棱DD1的中点时,会使得EF⊥B1C.下面证明:…(2分)∵E、F分别为棱DD1、BD的中点,∴EF∥BD1,…(3分)
∵B1C⊥BC1,B1C⊥C1D1,又BC1∩C1D1=C1,∴B1C⊥平面BC1D1,∴B1C⊥BD1
同理可得B1C⊥BD,又BD∩BD1=B,
故BD1⊥平面AB1C,所以B1C⊥BD1…(5分)
即EF⊥B1C;…(6分)
(2)由(1)可知:EF⊥B1C,又EF⊥FC,故EF⊥平面B1CF,
又EF=
| 1 |
| 2 |
| 3 |
CF=
| 2 |
| 2 |
| 6 |
故S△B1CF=
| 1 |
| 2 |
| 2 |
| 6 |
| 3 |
故三棱锥B1-EFC的体积为V=
| 1 |
| 3 |
| 3 |
| 3 |
点评:本题以正方体为载体考查线面垂直的证明以及三棱锥体积的求解,属中档题.

练习册系列答案
相关题目
在棱长为2的正方体AC1中,G是AA1的中点,则BD到平面GB1D1的距离是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( )
如图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( ) (理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F.
(理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F. (2007•上海)如图,在棱长为2的正方体ABCD-A'B'C'D'中,E,F分别是A'B'和AB的中点,求异面直线A'F与CE所成角的大小 (结果用反三角函数值表示).
(2007•上海)如图,在棱长为2的正方体ABCD-A'B'C'D'中,E,F分别是A'B'和AB的中点,求异面直线A'F与CE所成角的大小 (结果用反三角函数值表示).