Question

已知f（x）=1-（x-a）（x-b）（a＜b），m，n是f（x）的零点，且m＜n，则实数a、b、m、n的大小关系是    ．

Answer 1

【答案】分析：令y=-（x-a）（x-b），则有f（x）=1+y．故把函数y=-（x-a）（x-b）的图象向上平移1个单位，即可得到函数f（x）的图象，结合图象判断实数a、b、m、n的大小关系．
解答：解：令y=-（x-a）（x-b），则有f（x）=1+y．
故把函数y=-（x-a）（x-b）的图象向上平移1个单位，即可得到函数f（x）的图象．
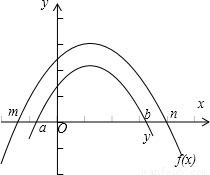
再由a＜b且m，n是f（x）的零点，m＜n，画出图象，如图所示：
故答案为 m＜a＜b＜n．

点评：本题主要考查二次函数的图象和性质，函数图象的平移变换，体现了数形结合的数学思想，属于基础题．