题目内容
已知f(x)=
,g(x)=
,
(Ⅰ)求y=g(x)的解析式,并画出其图象;
(Ⅱ)写出方程xf[g(x)]=2g[f(x)]的解集.
|
| 3f(x-1)-f(x-2) |
| 2 |
(Ⅰ)求y=g(x)的解析式,并画出其图象;
(Ⅱ)写出方程xf[g(x)]=2g[f(x)]的解集.
分析:(Ⅰ)直接利用条件对x-1以及x-2与0和1的大小关系分三种情况讨论,即可求出y=g(x)的解析式,并根据其解析式画出对应图象;
(Ⅱ)把方程xf[g(x)]=2g[f(x)]转化为x2=
即可求出其解集.
(Ⅱ)把方程xf[g(x)]=2g[f(x)]转化为x2=
|
解答: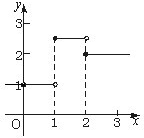 解:(Ⅰ)当x<1时,x-1<0,x-2<0,
解:(Ⅰ)当x<1时,x-1<0,x-2<0,
∴g(x)=
=1.
当1≤x<2时,x-1≥0,x-2<0,
∴g(x)=
=
.
当x≥2时,x-1>0,x-2≥0,
∴g(x)=
=2.故y=g(x)=
(3分)
其图象如右图.(3分)
(Ⅱ)∵g(x)>0,
∴f[g(x)]=2,x∈R
所以,方程xf[g(x)]=2g[f(x)]为x2=
其解集为{-
,2} (5分)
 解:(Ⅰ)当x<1时,x-1<0,x-2<0,
解:(Ⅰ)当x<1时,x-1<0,x-2<0,∴g(x)=
| 3-1 |
| 2 |
当1≤x<2时,x-1≥0,x-2<0,
∴g(x)=
| 6-1 |
| 2 |
| 5 |
| 2 |
当x≥2时,x-1>0,x-2≥0,
∴g(x)=
| 6-2 |
| 2 |
|
其图象如右图.(3分)
(Ⅱ)∵g(x)>0,
∴f[g(x)]=2,x∈R
所以,方程xf[g(x)]=2g[f(x)]为x2=
|
其解集为{-
| 5 |
点评:本题主要考查了分段函数解析式的求法及其应用以及分类讨论思想,转化思想的应用.在解决分段函数问题时,一定要看其定义在哪一段,再代入解析式,避免出错.

练习册系列答案
相关题目
 已知f(x)=
已知f(x)= ,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间 上的值域为
上的值域为 ,若存在,求出a的值;若不存在,请说明理由.
,若存在,求出a的值;若不存在,请说明理由. B.命题p:“∃x∈R,使得x2+x+1<0”,则 p:“∀x∈R,均有x2+x+1≥0”
B.命题p:“∃x∈R,使得x2+x+1<0”,则 p:“∀x∈R,均有x2+x+1≥0”