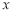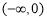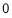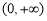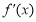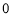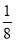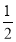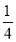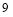题目内容
已知函数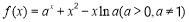
(1)求函数 在点(0,f(0))处的切线方程;
在点(0,f(0))处的切线方程;
(2)求函数 单调递增区间;
单调递增区间;
(3)若
 ∈[1,1],使得
∈[1,1],使得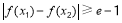 (e是自然对数的底数),求实数
(e是自然对数的底数),求实数 的取值范围.
的取值范围.
(1)函数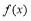 在点
在点 处的切线方程为
处的切线方程为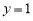 ; (2)函数
; (2)函数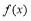 单调递增区间
单调递增区间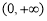 ;
;
(3)实数a的取值范围是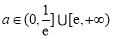 .
.
【解析】
试题分析:⑴ 先根据函数解析式求出 ,把
,把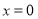 代入求出斜率,进而求得切线方程;⑵ 因为当
代入求出斜率,进而求得切线方程;⑵ 因为当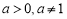 时,总有
时,总有 在
在 上是增函数, 又
上是增函数, 又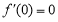 ,所以函数
,所以函数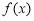 的单调增区间为
的单调增区间为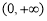 ;⑶ 要使
;⑶ 要使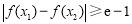 成立,只需
成立,只需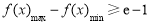 成立即可;再分
成立即可;再分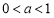 和
和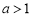 两种情况讨论即可.
两种情况讨论即可.
试题解析:⑴ 因为函数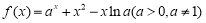 ,
,
所以 ,
, , 2分
, 2分
又因为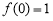 ,所以函数
,所以函数 在点
在点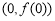 处的切线方程为
处的切线方程为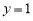 . 4分
. 4分
⑵ 由⑴,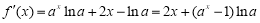 .
.
因为当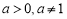 时,总有
时,总有 在
在 上是增函数,
上是增函数,
又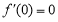 ,所以不等式
,所以不等式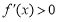 的解集为
的解集为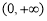 ,
,
故函数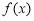 的单调增区间为
的单调增区间为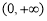 8分
8分
⑶ 因为存在 ,使得
,使得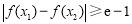 成立,
成立,
而当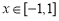 时,
时,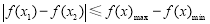 ,
,
所以只要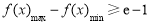 即可 9分
即可 9分
又因为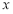 ,
,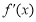 ,
,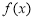 的变化情况如下表所示:
的变化情况如下表所示:
|
|
|
|
|
|
|
|
| 减函数 | 极小值 | 增函数 |
所以 在
在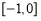 上是减函数,在
上是减函数,在 上是增函数,所以当
上是增函数,所以当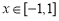 时,
时,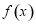 的最小值
的最小值
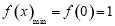 ,
, 的最大值
的最大值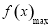 为
为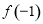 和
和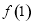 中的最大值.
中的最大值.
因为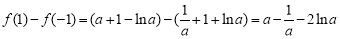 ,
,
令 ,因为
,因为 ,
,
所以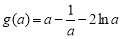 在
在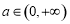 上是增函数.
上是增函数.
而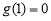 ,故当
,故当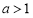 时,
时,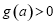 ,即
,即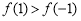 ;
;
当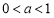 时,
时,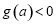 ,即
,即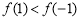 .
.
所以,当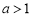 时,
时,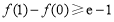 ,即
,即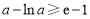 ,函数
,函数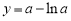 在
在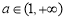 上是增函数,解得
上是增函数,解得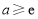 ;当
;当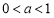 时,
时,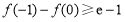 ,即
,即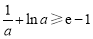 ,函数
,函数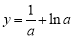 在
在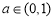 上是减函数,解得
上是减函数,解得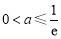 .
.
综上可知,所求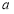 的取值范围为
的取值范围为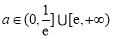 13分
13分
考点:导数的几何意义、导数的应用、构造法的应用.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目