题目内容
11.化简:(a${\;}^{\frac{2}{3}}$b${\;}^{\frac{1}{2}}$)(-3a${\;}^{\frac{1}{2}}$b${\;}^{\frac{2}{3}}$)÷($\frac{1}{3}$a${\;}^{\frac{1}{6}}$b${\;}^{\frac{5}{6}}$)=-9a${b}^{\frac{1}{3}}$.分析 利用指数幂的运算法则即可得出.
解答 解:原式=$\frac{-3}{\frac{1}{3}}$${a}^{\frac{2}{3}+\frac{1}{2}-\frac{1}{6}}$${b}^{\frac{1}{2}+\frac{2}{3}-\frac{5}{6}}$
=-9a${b}^{\frac{1}{3}}$.
故答案为:-9a${b}^{\frac{1}{3}}$.
点评 本题考查了指数幂的运算法则,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知函数f(x)=$\frac{1}{x+1}$,则函数f(x)的定义域是( )
| A. | {x|x≠1} | B. | {x|x≠0} | C. | {x|x≠-1} | D. | x∈R |
19.数据5,7,7,8,10,11的方差是( )
| A. | 24 | B. | 10 | C. | 4 | D. | 2 |
6.在正项等比数列{an}中,10a1,$\frac{1}{2}{a_3},3{a_2}$成等差数列,则$\frac{{{a_8}+{a_{10}}+{a_{11}}}}{{{a_6}+{a_8}+{a_9}}}$=( )
| A. | 5 | B. | 4 | C. | 25 | D. | 4或25 |
3.已知f(x)=$\left\{\begin{array}{l}{a{x}^{2}+x}&{x≥0}\\{-a{x}^{2}+x}&{x<0}\end{array}\right.$,当x∈[-$\frac{1}{4}$,$\frac{1}{4}$]时恒有f(x+a)<f(x),则实数a的取值范围是( )
| A. | ($\frac{1-\sqrt{17}}{4},0$) | B. | [-2,0) | C. | (-∞,-$\sqrt{2}$) | D. | [-2,-$\sqrt{2}$] |
20.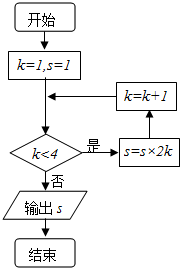 执行如图所示的程序框图,输出的s值为( )
执行如图所示的程序框图,输出的s值为( )
 执行如图所示的程序框图,输出的s值为( )
执行如图所示的程序框图,输出的s值为( )| A. | 8 | B. | 16 | C. | 48 | D. | 64 |