题目内容
下列命题中,真命题的有_________(只填写真命题的序号)
①若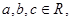 则“
则“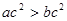 ”是“
”是“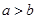 ”成立的充分不必要条件;
”成立的充分不必要条件;
② 当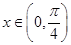 时,函数
时,函数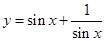 的最小值为2;
的最小值为2;
③ 若命题“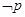 ”与命题“
”与命题“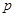 或
或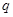 ”都是真命题,则命题
”都是真命题,则命题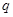 一定是真命题;
一定是真命题;
④ 若命题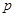 :
: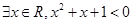 ,则
,则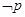 :
: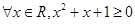 .
.
【答案】
①②④
【解析】
试题分析:由 可得
可得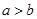 ,但反之不能,即“①若
,但反之不能,即“①若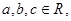 则“
则“ ”是“
”是“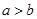 ”成立的充分不必要条件”是真命题;
”成立的充分不必要条件”是真命题;
② 当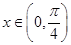 时,函数
时,函数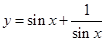 的最小值为2是假命题,因为应用均值定理等号成立的条件是
的最小值为2是假命题,因为应用均值定理等号成立的条件是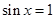 ,不可能;
,不可能;
因为命题“ ”与命题“
”与命题“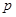 或
或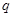 ”都是真命题,所以p是假命题,q是真命题,即“③ 若命题“
”都是真命题,所以p是假命题,q是真命题,即“③ 若命题“ ”与命题“
”与命题“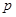 或
或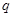 ”都是真命题,则命题
”都是真命题,则命题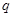 一定是真命题;”是真命题;
一定是真命题;”是真命题;
因为存在性命题的否定是全称命题,所以“④ 若命题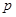 :
: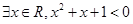 ,则
,则 :
: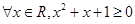 .”是真命题;综上知,答案为①②④。
.”是真命题;综上知,答案为①②④。
考点:本题综合考查命题的概念,充要条件的概念,三角函数的最值。
点评:小综合题,涉及命题真假判断的题目,往往综合性较强,考查的覆盖面较广。存在性命题的否定是全称命题。

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
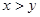 ,则
,则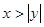 ”的逆命题
”的逆命题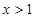 ,则
,则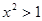 ”的否命题
”的否命题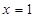 ,则
,则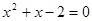 ”的否命题
”的否命题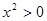 ,则
,则