题目内容
已知点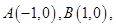 直线AM,BM相交于点M,且
直线AM,BM相交于点M,且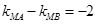
(1)求点M的轨迹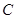 的方程;
的方程;
(2)过定点(0,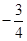 )作直线PQ与曲线C交于P,Q两点,求
)作直线PQ与曲线C交于P,Q两点,求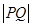 的最小值
的最小值
(1)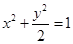
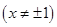 ; (2)
; (2)
解析试题分析:(1)先设出点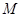 的坐标,根据两点间的斜率公式求出
的坐标,根据两点间的斜率公式求出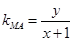 和
和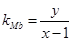 ,代入已知条件
,代入已知条件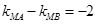 中,化简整理得
中,化简整理得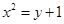
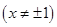 ,限制条件一定要有;(2)先设出直线
,限制条件一定要有;(2)先设出直线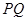 的方程,以及点
的方程,以及点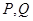 的坐标,直线方程与曲线方程联立方程组可得
的坐标,直线方程与曲线方程联立方程组可得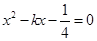 ,根据根与系数的关系求得
,根据根与系数的关系求得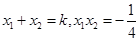 ,将此式代入
,将此式代入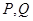 两点间的距离公式,化简得
两点间的距离公式,化简得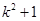 ,根据二次函数的性质判断此式的取值即可
,根据二次函数的性质判断此式的取值即可
试题解析:(1)解:设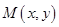 , 1分
, 1分
则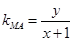 ,
,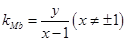 , 3分
, 3分
∴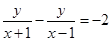 , 4分
, 4分
∴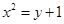
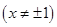 6分 (条件1分)
6分 (条件1分)
(2) 显然直线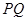 的斜率存在,设直线
的斜率存在,设直线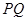 的方程是
的方程是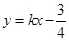 ,
,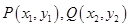 ,
,
则直线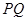 的方程为:
的方程为: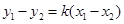 , 8分
, 8分
联立 ,消去y得
,消去y得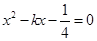 9分
9分
∵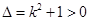 ,∴
,∴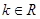 , 10分
, 10分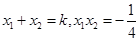 , 11分
, 11分
∴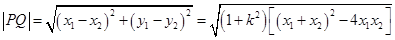
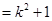 12分
12分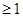 ,当且仅当
,当且仅当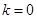 时取等号,此时
时取等号,此时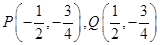 , 13分
, 13分
所以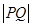 的最小值是1 14分
的最小值是1 14分
考点:1 直线的斜率;2 方程的根与系数的关系;3 轨迹方程;4 两点间的距离公式;5 直线方程

练习册系列答案
相关题目
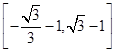 ,求直线AB的倾斜角α的取值范围.
,求直线AB的倾斜角α的取值范围. 的顶点
的顶点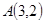 ,
,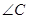 的平分线
的平分线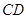 所在直线方程为
所在直线方程为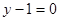 ,
,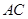 边上的高
边上的高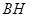 所在直线方程为
所在直线方程为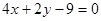 .
.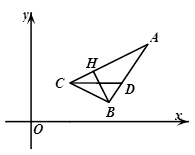
 的坐标;
的坐标;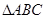 的面积.
的面积.  的交点M,且满足下列条件的直线方程:
的交点M,且满足下列条件的直线方程: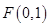 直线
直线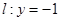 ,
,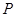 为平面上的动点,过点
为平面上的动点,过点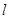 的垂线,垂足为
的垂线,垂足为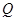 ,且
,且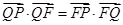 .
. 、
、 是轨迹
是轨迹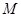 上异于坐标原点
上异于坐标原点 的不同两点,轨迹
的不同两点,轨迹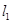 、
、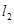 ,且
,且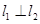 ,
,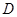 ,求点
,求点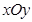 中,已知圆
中,已知圆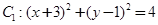 和圆
和圆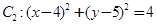 .
. 过点
过点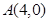 ,且被圆
,且被圆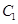 截得的弦长为
截得的弦长为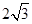 ,求直线
,求直线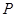 为平面上的点,满足:存在过点
为平面上的点,满足:存在过点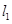 和
和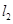 ,它们分别与圆
,它们分别与圆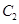 相交,且直线
相交,且直线 的直线方程.
的直线方程.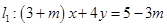 ,
,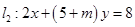 ;
; 为何值时,
为何值时,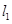 与
与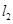 (1)相交;(2)平行;(3)垂直.
(1)相交;(2)平行;(3)垂直.