题目内容
如图,请观察杨辉三角(杨辉是我国南宋时期的数学家)中各数排列的特征,其中沿箭头所示的数依次组成一个锯齿形数列:1、1、2、3、3、6、4、10、5、…,设此数列的前n项和为Sn,则S2004-2S2005+S2006等于( )
A.502501
B.520502
C.502503
D.以上都不对
【答案】分析:根据杨辉三角的生成过程cnm-1+cnm=cn=1m,分奇偶讨论,求出数列的通项公式,
解答:解:杨辉三角形的生成过程,
n为偶数时,an=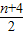 ,
,
n为奇数时,a1=1.a3=3,an+2=an+an-1=an+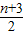
∴a3-a1=2,
a5-a3=3,
…
an-an-2= ,
,
an=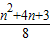 .
.
∴S2004-2S2005+S2006=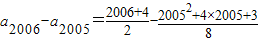
=51376
故选D.
点评:考查杨辉三角的产生过程及数列求和问题,有关数列求和问题的解决方法和途径,要紧抓数列的通项公式,在求数列通项公式的时,体现了分类讨论的思想.
解答:解:杨辉三角形的生成过程,
n为偶数时,an=
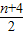 ,
,n为奇数时,a1=1.a3=3,an+2=an+an-1=an+
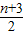
∴a3-a1=2,
a5-a3=3,
…
an-an-2=
 ,
,an=
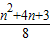 .
.∴S2004-2S2005+S2006=
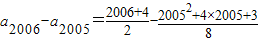
=51376
故选D.
点评:考查杨辉三角的产生过程及数列求和问题,有关数列求和问题的解决方法和途径,要紧抓数列的通项公式,在求数列通项公式的时,体现了分类讨论的思想.

练习册系列答案
相关题目
 如图,请观察杨辉三角(杨辉是我国南宋时期的数学家)中各数排列的特征,其中沿箭头所示的数依次组成一个锯齿形数列:1、1、2、3、3、6、4、10、5、…,设此数列的前n项和为Sn,则S2004-2S2005+S2006等于( )
如图,请观察杨辉三角(杨辉是我国南宋时期的数学家)中各数排列的特征,其中沿箭头所示的数依次组成一个锯齿形数列:1、1、2、3、3、6、4、10、5、…,设此数列的前n项和为Sn,则S2004-2S2005+S2006等于( )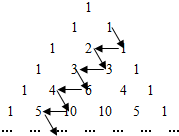 如图,请观察杨辉三角(杨辉是我国南宋时期的数学家)中各数排列的特征,其中沿箭头所示的数依次组成一个锯齿形数列:1、1、2、3、3、6、4、10、5、…,设此数列的前n项和为Sn,则S2004-2S2005+S2006等于
如图,请观察杨辉三角(杨辉是我国南宋时期的数学家)中各数排列的特征,其中沿箭头所示的数依次组成一个锯齿形数列:1、1、2、3、3、6、4、10、5、…,设此数列的前n项和为Sn,则S2004-2S2005+S2006等于