题目内容
给出以下五个命题,其中所有正确命题的序号为①函数
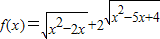 的最小值为l+2
的最小值为l+2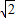 ;
;②已知函数f (x)=|x2-2|,若f (a)=f (b),且0<a<b,则动点P(a,b)到直线4x+3y-15=0的距离的最小值为1;
③命题“函数f(x)=xsinx+1,当x1,x2∈
 ,且|x1|>|x2|时,有f (x1)>f(x2)”是真命题;
,且|x1|>|x2|时,有f (x1)>f(x2)”是真命题;④“
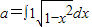 ”是函数“y=cos2(ax)-sin2(ax)的最小正周期为4”的充要条件;
”是函数“y=cos2(ax)-sin2(ax)的最小正周期为4”的充要条件;⑤已知等差数列{an}的前n项和为Sn,
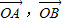 为不共线向量,又
为不共线向量,又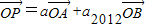 ,若
,若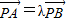 ,则S2012=2013.
,则S2012=2013.
【答案】分析:分析①中函数的单调性及定义域,可求出①中函数的最小值,进而判断①的真假;
分析②中函数f (x)=|x2-2|图象和性质及已知中f (a)=f (b),且0<a<b,可判断出动点P(a,b)的轨迹方程,分析曲线上点到直线距离的最值,可得答案;
分析③中函数的奇偶性及单调性,即可判断出|x1|>|x2|时,f (x1)与f(x2)的大小,进而判断③的真假;
分析④中,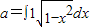 的值,及y=cos2(ax)-sin2(ax)的最小正周期为4时,对应的a值,比较后根据充要条件的定义可得答案;
的值,及y=cos2(ax)-sin2(ax)的最小正周期为4时,对应的a值,比较后根据充要条件的定义可得答案;
根据三点共线的充要条件,分析出a+a2012=1,进而根据前n项和公式求出S2012,即可判断⑤的真假.
解答:解:①中函数 的定义域为{x|x≥4或x≤0}.
的定义域为{x|x≥4或x≤0}.
又x∈[4,+∞)时,f(x)单调递增,⇒f(x)≥f(4)=1+2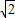 ;
;
而x∈(-∞,0]时,f(x)单调递减,⇒f(x)≥f(0)=0+4=4;
故最小值为1+2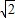 ,
,
故①正确;
②中,由题意可得0<a<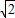 <b,f (a)=2-a2,f (b)=b2-2,
<b,f (a)=2-a2,f (b)=b2-2,
∴a2+b2=4(0<a< <b),
<b),
其图象为一段圆弧,由于弧a2+b2=4(0≤a≤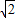 ≤b)到直线4x+3y-15=0的距离的最小的点为(
≤b)到直线4x+3y-15=0的距离的最小的点为( ,
, )
)
但弧a2+b2=4(0<a<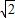 <b)不含(
<b)不含(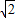 ,
, )点
)点
故②错误;
③中,函数f(x)=xsinx+1为偶函数,且在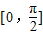 上为增函数
上为增函数
故当|x1|>|x2|时,有f (x1)>f(x2),
故③正确;
④中, =
=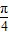 ,则y=cos2(ax)-sin2(ax)的最小正周期为4,
,则y=cos2(ax)-sin2(ax)的最小正周期为4,
但当y=cos2(ax)-sin2(ax)的最小正周期为4,a=±
故“ ”是函数“y=cos2(ax)-sin2(ax)的最小正周期为4”的充分不必要条件;
”是函数“y=cos2(ax)-sin2(ax)的最小正周期为4”的充分不必要条件;
故④错误;
⑤中,若 ,则P,A,B三点共线
,则P,A,B三点共线
又 ,
,
∴a+a2012=1
∴S2012=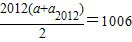 ≠2013
≠2013
故⑤错误
故答案为:①③
点评:本题是一个函数性质及数列的综合题,难度稍大,熟练掌握函数的定义域、值域(最值)的求法,函数的单调性、奇偶性,充要条件的定义,向量法三点共线的充要条件及数据的前n项和公式是解答的关键.
分析②中函数f (x)=|x2-2|图象和性质及已知中f (a)=f (b),且0<a<b,可判断出动点P(a,b)的轨迹方程,分析曲线上点到直线距离的最值,可得答案;
分析③中函数的奇偶性及单调性,即可判断出|x1|>|x2|时,f (x1)与f(x2)的大小,进而判断③的真假;
分析④中,
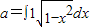 的值,及y=cos2(ax)-sin2(ax)的最小正周期为4时,对应的a值,比较后根据充要条件的定义可得答案;
的值,及y=cos2(ax)-sin2(ax)的最小正周期为4时,对应的a值,比较后根据充要条件的定义可得答案;根据三点共线的充要条件,分析出a+a2012=1,进而根据前n项和公式求出S2012,即可判断⑤的真假.
解答:解:①中函数
 的定义域为{x|x≥4或x≤0}.
的定义域为{x|x≥4或x≤0}.又x∈[4,+∞)时,f(x)单调递增,⇒f(x)≥f(4)=1+2
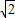 ;
;而x∈(-∞,0]时,f(x)单调递减,⇒f(x)≥f(0)=0+4=4;
故最小值为1+2
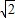 ,
,故①正确;
②中,由题意可得0<a<
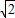 <b,f (a)=2-a2,f (b)=b2-2,
<b,f (a)=2-a2,f (b)=b2-2,∴a2+b2=4(0<a<
 <b),
<b),其图象为一段圆弧,由于弧a2+b2=4(0≤a≤
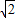 ≤b)到直线4x+3y-15=0的距离的最小的点为(
≤b)到直线4x+3y-15=0的距离的最小的点为( ,
, )
)但弧a2+b2=4(0<a<
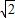 <b)不含(
<b)不含(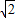 ,
, )点
)点故②错误;
③中,函数f(x)=xsinx+1为偶函数,且在
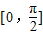 上为增函数
上为增函数故当|x1|>|x2|时,有f (x1)>f(x2),
故③正确;
④中,
 =
=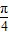 ,则y=cos2(ax)-sin2(ax)的最小正周期为4,
,则y=cos2(ax)-sin2(ax)的最小正周期为4,但当y=cos2(ax)-sin2(ax)的最小正周期为4,a=±

故“
 ”是函数“y=cos2(ax)-sin2(ax)的最小正周期为4”的充分不必要条件;
”是函数“y=cos2(ax)-sin2(ax)的最小正周期为4”的充分不必要条件;故④错误;
⑤中,若
 ,则P,A,B三点共线
,则P,A,B三点共线又
 ,
,∴a+a2012=1
∴S2012=
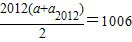 ≠2013
≠2013故⑤错误
故答案为:①③
点评:本题是一个函数性质及数列的综合题,难度稍大,熟练掌握函数的定义域、值域(最值)的求法,函数的单调性、奇偶性,充要条件的定义,向量法三点共线的充要条件及数据的前n项和公式是解答的关键.

练习册系列答案
相关题目
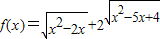 的最小值为l+2
的最小值为l+2 ;
; ,且|x1|>|x2|时,有f (x1)>f(x2)”是真命题;
,且|x1|>|x2|时,有f (x1)>f(x2)”是真命题; ”是函数“y=cos2(ax)-sin2(ax)的最小正周期为4”的充要条件;
”是函数“y=cos2(ax)-sin2(ax)的最小正周期为4”的充要条件; 为不共线向量,又
为不共线向量,又 ,若
,若 ,则S2012=2013.
,则S2012=2013.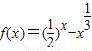 在区间(0、1)上存在零点
在区间(0、1)上存在零点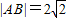
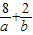 最小值为9.
最小值为9.