题目内容
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() .
.
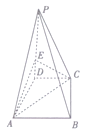
(1)在![]() 上确定一点
上确定一点![]() ,使得
,使得![]() 平面
平面![]() ,并求
,并求![]() 的值;
的值;
(2)在(1)条件下,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:对问题(1),可连接![]() 交
交![]() 于
于![]() ,根据线面平行的判定定理并结合三角形相似即可在
,根据线面平行的判定定理并结合三角形相似即可在![]() 上确定一点
上确定一点![]() ,进而可求
,进而可求![]() 的值;对问题(2),可通过建立空间直角坐标系,并分别求出平面
的值;对问题(2),可通过建立空间直角坐标系,并分别求出平面![]() 与平面
与平面![]() 的法向量,进而可求得平面
的法向量,进而可求得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
试题解析:(1)连接![]() 交
交![]() 于
于![]() ,
,
在![]() 中,过
中,过![]() 作
作![]() 交
交![]() 于
于![]() ,.
,.
∵![]() 平面
平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() ,∴
,∴![]()
(2)以![]() 为坐标原点,建立如图所示的空间直角坐标系,则
为坐标原点,建立如图所示的空间直角坐标系,则
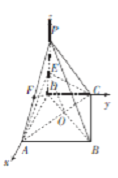
![]() ,
,
所以![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则
 ,即
,即![]() ,
,
令![]() ,则
,则![]() ,∴
,∴![]()
取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() ,则
,则![]() 平面
平面![]() ,
,
即![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
∴
∴平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]()

练习册系列答案
相关题目
【题目】某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
组别 | 频数 | 频率 |
145.5~149.5 | 8 | 0.16 |
149.5~153.5 | 6 | 0.12 |
153.5~157.5 | 14 | 0.28 |
157.5~161.5 | 10 | 0.20 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 |
|
|
合计 |
|
|
(1)求出表中字母![]() 所对应的数值;
所对应的数值;
(2)在给出的直角坐标系中画出频率分布直方图;
(3)估计该校高一女生身高在149.5~165.5![]() 范围内有多少人?
范围内有多少人?