题目内容
已知数列![]() 满足
满足![]()
求数列![]() 的通项公式;
的通项公式;
设b![]() =
=![]() (n∈N
(n∈N![]() ,n≥2), b
,n≥2), b![]() ,求证:b
,求证:b![]() +b
+b![]() +……+b
+……+b![]() < 3 .
< 3 .
(1);(2)同解析;
解析:
(1)∵![]() ∴
∴![]()
∴数列{![]() }是以首项a1+1,公比为2的等比数列,
}是以首项a1+1,公比为2的等比数列,
即![]()
![]()
(2)b![]() =
=![]() =
=![]() =
=
![]() ≤
≤![]() (n≥2)
(n≥2)
∴b![]() +b
+b![]() +……+b
+……+b![]() =1+
=1+![]()
![]()
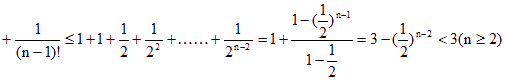
n=1时,b![]() =1<3 成立, 所以b
=1<3 成立, 所以b![]() +b
+b![]() +……+b
+……+b![]() < 3
< 3

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
题目内容
已知数列![]() 满足
满足![]()
求数列![]() 的通项公式;
的通项公式;
设b![]() =
=![]() (n∈N
(n∈N![]() ,n≥2), b
,n≥2), b![]() ,求证:b
,求证:b![]() +b
+b![]() +……+b
+……+b![]() < 3 .
< 3 .
(1);(2)同解析;
(1)∵![]() ∴
∴![]()
∴数列{![]() }是以首项a1+1,公比为2的等比数列,
}是以首项a1+1,公比为2的等比数列,
即![]()
![]()
(2)b![]() =
=![]() =
=![]() =
=
![]() ≤
≤![]() (n≥2)
(n≥2)
∴b![]() +b
+b![]() +……+b
+……+b![]() =1+
=1+![]()
![]()
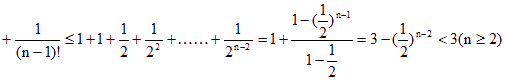
n=1时,b![]() =1<3 成立, 所以b
=1<3 成立, 所以b![]() +b
+b![]() +……+b
+……+b![]() < 3
< 3

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案