题目内容
(14分)已知数列 的前n项和为
的前n项和为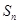 ,
, ,
, ,等差数列
,等差数列 中
中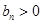
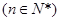 ,且
,且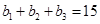 ,又
,又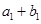 、
、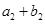 、
、 成等比数列.
成等比数列.
(Ⅰ)求数列 、
、 的通项公式;
的通项公式;
(Ⅱ)求数列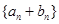 的前n项和Tn.
的前n项和Tn.
【答案】
(1) ,bn=2n+1
,bn=2n+1 (2)
(2)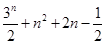
【解析】(Ⅰ)∵ ,
, ,
,
∴ ,
,
∴ ,
,
∴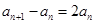 ,
,
∴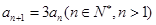 …………………………3分
…………………………3分
而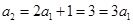 ,∴
,∴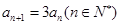
∴数列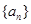 是以1为首项,3为公比的等比数列,
是以1为首项,3为公比的等比数列,
∴ …………………………5分
…………………………5分
∴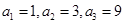 ,
,
在等差数列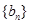 中,∵
中,∵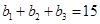 ,∴
,∴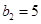 。
。
又因 、
、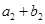 、
、 成等比数列,设等差数列
成等比数列,设等差数列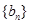 的公差为d,
的公差为d,
∴(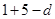 )
)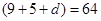 ………………………………7分
………………………………7分
解得d=-10,或d=2,
∵
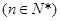 ,∴舍去d=-10,取d=2, ∴b1=3,
,∴舍去d=-10,取d=2, ∴b1=3,
∴bn=2n+1 , ………………………………9分
, ………………………………9分
(Ⅱ)由(Ⅰ)知
∴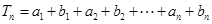
=(
=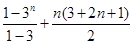
=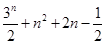 ………………………………14分
………………………………14分

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 求使不等式
求使不等式 的前n项和为
的前n项和为 ,
, 且满足
且满足 +n (n>1且n∈
+n (n>1且n∈ )
) ,求使得不等式
,求使得不等式 成立的最小正整数n的值
成立的最小正整数n的值  的前n项和为
的前n项和为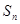 ,且
,且 ,
, ,并猜想
,并猜想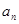 的表达式。
的表达式。