题目内容
已知a、b都是正数,且a≤2,b≤2,则a2-2b为非负数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:先根据约束条件画出可行域,再利用几何概型求概率,为了求出不规则图形的面积,只需求出函数y=
x2在[0,2]上的积分即可.
| 1 |
| 2 |
解答: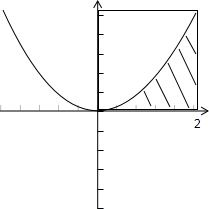 解:由题意得:
解:由题意得:
在坐标系aOb系中画出图形,
图中阴影部分的面积=
x2dx=
x3
=
,
∴则a2-2b为非负数的概率=
=
.
故选B.
 解:由题意得:
解:由题意得:
|
在坐标系aOb系中画出图形,
图中阴影部分的面积=
| ∫ | 2 0 |
| 1 |
| 2 |
| 1 |
| 6 |
| | | 2 0 |
| 4 |
| 3 |
∴则a2-2b为非负数的概率=
| ||
| 2×2 |
| 1 |
| 3 |
故选B.
点评:单纯线性规划题在高考题中越来越少出现,因为没有太多新意,但并不是不考了,而是与其他知识点结合应用,此题就有这个特点.

练习册系列答案
相关题目
已知a,b都是正数,下列命题正确的是( )
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
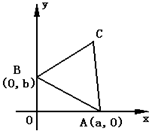 已知a,b都是正数,△ABC是平面直角坐标系xOy内,以两点A ( a,0 )和B ( 0,b )为顶点的正三角形,且它的第三个顶点C在第一象限内.
已知a,b都是正数,△ABC是平面直角坐标系xOy内,以两点A ( a,0 )和B ( 0,b )为顶点的正三角形,且它的第三个顶点C在第一象限内.