Question

（本小题满分12分）

有两枚大小相同、质地均匀的正四面体玩具，每个玩具的各个面上分别写着数字1，2，3，5.同时投掷这两枚玩具一次，记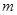为两个朝下的面上的数字之和.

   （Ⅰ）求事件“m不小于6”的概率；

   （Ⅱ）“m为奇数”的概率和“m为偶数”的概率是不是相等？证明你作出的结论.

 

Answer 1

【答案】

（1）P(m≥6)= ；

   （2）“m为奇数”的概率和“m为偶数”的概率不相等.

         因为m为奇数的概率为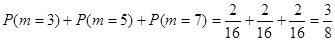 10分

         M为偶数的概率为.这两个概率值不相等 。

【解析】（I）本小题属于古典概型概率问题，只需求出总的基本事件的个数，然后求出事件“m不小于6”包含的基本事件的个数，再根据概率计算公式计算即可.

（II）m为奇数和偶数的概率也属于古典概型概率问题，做法同（I），然后比较“m为奇数”的概率和“m为偶数”的概率，即可判断是不是相等.

解：因玩具是均匀的，所以玩具各面朝下的可能性相等，出现的可能情况有

    （1，1），（1，2），（1，3），（1，5），（2，1），（2，2），（2，3），（2，5）

    （3，1），（3，2），（3，3），（3，5），（5，1），（5，2），（5，3），（5，5）

         共16种       4分

         （1）事件“m不小于6”包含其中（1，5），（2，5），（3，5），（3，3）（5，1），（5，2），（5，3），（5，8）共8个基本事件      6分

         所以P(m≥6)=         8分

   （2）“m为奇数”的概率和“m为偶数”的概率不相等.

         因为m为奇数的概率为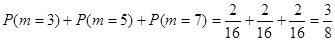 10分

         M为偶数的概率为.这两个概率值不相等   12分