题目内容
如图,正方体ABCD—A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.

(1)求GH长的取值范围;
(2)当GH取得最小值时,求证:EH与FG共面;并求出此时EH与FG的交点P到直线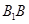 的距离.
的距离.
【答案】
(1)[2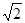 ,4] (2)
,4] (2)
【解析】
试题分析:解:(1)以D为原点,DA,DC,DD1分别为x轴,y轴,z轴建立空间直角坐标系.
设DG=a,DH=b,则E(4,0,4),F(0,4,4),G(a,0,0),H(0,b,0).
∴ =(-4,b,-4),
=(-4,b,-4),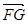 =(a,-4,-4).
=(a,-4,-4).
∵EH⊥FG.
∴ ·
·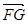 =-4a-4b+16=0,则a+b=4,即b=4-a.
=-4a-4b+16=0,则a+b=4,即b=4-a.
又G1H在棱DA,DC上,则0≤a≤8,0≤b≤8,从而0≤a≤4.
∴GH=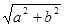 =
= .
.
∴GH取值范围是[2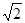 ,4] . ……6分
,4] . ……6分
(2)当GH=2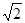 时,a=2,b=2.
时,a=2,b=2.
∴ =(-2,2,0),
=(-2,2,0), =(-4,4,0),即
=(-4,4,0),即 =2
=2 .
.
∴EF∥GH,即EH与FG共面.
所以EF=2GH,EF∥GH,则 .
.
设P(x1,y1,z1),则 =(x1-4,y,z1-4).
=(x1-4,y,z1-4).
∴x1= ,y1=
,y1= ,z1=
,z1= ,即P(
,即P( ,
, ,
, ).
).
则P( ,
, ,
, )在底面上ABCD上的射影为M(
)在底面上ABCD上的射影为M( ,
, ,0).又B(8,8,0),
,0).又B(8,8,0),
所以 为点P到直线
为点P到直线 的距离. ……12分
的距离. ……12分
考点:空间中两点的距离,点到直线的距离
点评:关键是通过建立空间直角坐标系,然后表示点的坐标以及点在平面的射影得到距离,属于基础题。

练习册系列答案
相关题目

 如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和A1D1的中点.证明:向量
如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和A1D1的中点.证明:向量 如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.
如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG. 如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( )
如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( ) 如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且
如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且