题目内容
(本小题满分12分)
图4是某城市通过抽样得到的居民某年的月均用水量(单位:吨)的频率分布直方图
(Ⅰ)求直方图中x的值
(II)若将频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样),求月均用水量在3至4吨的居民数X的分布列和数学期望。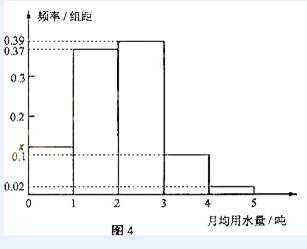
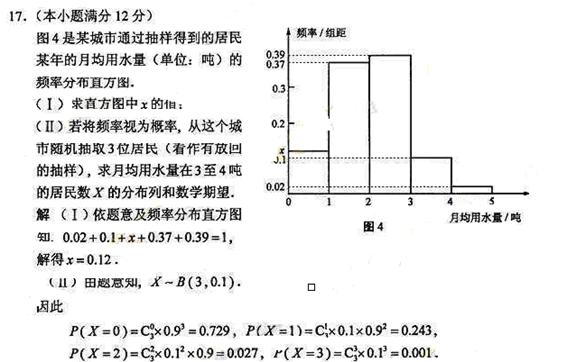

解析

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
(本小题满分12分)
在调查学生数学成绩与物理成绩之间的关系时,得到如下数据(人数):
| | 物理成绩好 | 物理成绩不好 | 合计 |
| 数学成绩好 | 20 | 30 | 50 |
| 数学成绩不好 | 40 | a | 60 |
| 合计 | 60 | 50 | 110 |
(1)根据上表确定a的值
(2)试判断数学成绩与物理成绩之间是否线性相关,判断出错的概率有多大?
参考公式
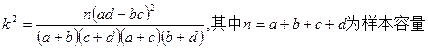
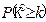 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(10分)假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:若由资料知,y对x呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
| x | 2 | 3 | 4 | 5 | 6 |
 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中个抽出500件,量其内径尺寸,的结果如下表:
甲厂
(1) 试分别估计两个分厂生产的零件的优质品率;
(2) 由于以上统计数据填下面 列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
| | 甲 厂 | 乙 厂 | 合计 |
| 优质品 | | | |
| 非优质品 | | | |
| 合计 | | | |



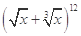 展开式中含的有理项共有( )
展开式中含的有理项共有( )
| A.1项 | B.2项 | C.3项 | D.4项 |
(本小题满分12分)
某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名学生进行调查,下表是这n名学生的日睡眠时间的频率分布表。
| 序号(i) | 分组(睡眠时间) | 频数(人数) | 频率 |
| 1 | [4,5) | 6 | 0.12 |
| 2 | [5,6) | | 0.20 |
| 3 | [6,7) | a | |
| 4 | [7,8) | b | |
| 5 | [8,9) | | 0.08 |
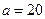 ,将表中数据补全,并画出频率分布直方图.
,将表中数据补全,并画出频率分布直方图.(2)统计方法中,同一组数据常用该组区间的中点值(例如区间
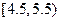 的中点值是5)作为代表.若据此计算的上述数据的平均值为7.2,求
的中点值是5)作为代表.若据此计算的上述数据的平均值为7.2,求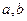 的值,并由此估计该学校学生的日平均睡眠时间在7.5小时以上的概率.
的值,并由此估计该学校学生的日平均睡眠时间在7.5小时以上的概率. 
 ;
; 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量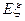 .(要求:答案用最简分数表示)
.(要求:答案用最简分数表示)