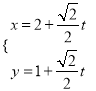题目内容
【题目】在平面直角坐标系xoy中,曲线C的参数方程是![]() (θ为参数).以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,直线l的极坐标方程为:
(θ为参数).以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,直线l的极坐标方程为:![]()
(1)求曲线C的极坐标方程;
(2)设直线θ=![]() 与直线l交于点M,与曲线C交于P,Q两点,已知|OM||OP||OQ)=10,求t的值。
与直线l交于点M,与曲线C交于P,Q两点,已知|OM||OP||OQ)=10,求t的值。
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)由曲线C的参数方程,可得曲线C的普通方程,再将其化为极坐标方程.
(2)将![]() 代入
代入![]() 中,求得|OM|,将
中,求得|OM|,将![]() 代入
代入![]() 中,得
中,得![]() ,得到|OP|
,得到|OP|![]() |OQ|=5.再根据|OM|
|OQ|=5.再根据|OM|![]() |OP|
|OP|![]() |OQ|=10,解得t值即可.
|OQ|=10,解得t值即可.
(1)由曲线C的参数方程,可得曲线C的普通方程为![]() ,
,
即![]() . ∵
. ∵ ![]() ,
,![]() ,
,
故曲线C的极坐标方程为![]() .
.
(2)将![]() 代入
代入![]() 中,得
中,得![]() ,则
,则![]() .
.
∴ |OM|=![]() .将
.将![]() 代入
代入![]() 中,得
中,得![]() .
.
设点P的极径为![]() ,点Q的极径为
,点Q的极径为![]() ,则
,则![]() . 所以|OP|
. 所以|OP|![]() |OQ|=5.又|OM|
|OQ|=5.又|OM|![]() |OP|
|OP|![]() |OQ|=10,则5
|OQ|=10,则5![]() =10.∴ t=
=10.∴ t=![]() 或
或![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目