题目内容
设函数![]()
![]() .
.
(1) 当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2) 当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最小值
上的最小值![]() 和最大值
和最大值![]() .
.
【解析】:![]() …………………………1分
…………………………1分
(1)当![]() 时
时![]()
![]() 恒成立,∴
恒成立,∴![]() 的单调递增区间为R. …………………………4分
的单调递增区间为R. …………………………4分
(2)当![]() 时,
时,![]() ,其开口向上,对称轴
,其开口向上,对称轴![]() ,且过
,且过![]()
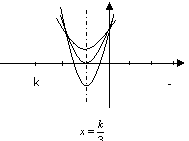 (i)当
(i)当![]() ,即
,即![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
从而当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,
,
当![]() 时,
时,![]() 取得最大值
取得最大值![]() .…………………………7分
.…………………………7分
(ii)当![]() ,即
,即![]() 时,令
时,令![]()
解得:![]() ,注意到
,注意到![]() ,
,
(注:可用韦达定理判断![]() ,
,![]() ,从而
,从而![]() ;或者由对称结合图像判断)
;或者由对称结合图像判断)
![]() …………………………10分
…………………………10分
![]() ,
,![]() 的最小值
的最小值![]() ,
,
![]()
![]() 的最大值
的最大值![]()
综上所述,当![]() 时,
时,![]() 的最小值
的最小值![]() ,最大值
,最大值![]() ……14分
……14分
解法2(2)当![]() 时,对
时,对![]() ,都有
,都有![]() ,故
,故![]() …………………………8分
…………………………8分
![]() 故
故![]() ,…………………………12分
,…………………………12分
而 ![]() ,
,![]()
所以 ![]() ,
,![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目