题目内容
已知函数f(x)=x3-2x,其中a-1≤x≤a+1,a∈R,设集合M={(m,f(n))|m,n∈[a-1,a+1]|},若f(x)单调递增,则S的最小值为分析:先研究函数的性质,是奇函数且x>
=
时,f(x)单调递增.再将面积表达出来,进而可求出S的最小值.
|
| ||
| 3 |
解答: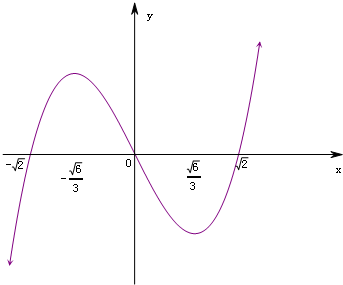 解:f(x)=x3-2x=x(x2-2)=0∴x=-
解:f(x)=x3-2x=x(x2-2)=0∴x=-
或0或
∵f(-x)=-f(x),∴f(x)为奇函数.
?0<x1<x2f(x1)-f(x2)=(x1-x2)(x12+x1x2+x22-2)>(x1-x2)(3x12-2)
当x>
=
时,f(x1)-f(x2)>0,f(x)单调递增.
由对称性画出草图n∈[a-1,a+1]
∵1<
<2,
∴m∈[a-1,a+1],f(n)为n∈[a-1,a+1]时的值域的长度d.要使f(n)的值域最小当a-1<-
<
<a+1时f(n)的值域最小,则d=f(-
)-f(
)=
S=2d=
,
故答案为
.
 解:f(x)=x3-2x=x(x2-2)=0∴x=-
解:f(x)=x3-2x=x(x2-2)=0∴x=-| 2 |
| 2 |
∵f(-x)=-f(x),∴f(x)为奇函数.
?0<x1<x2f(x1)-f(x2)=(x1-x2)(x12+x1x2+x22-2)>(x1-x2)(3x12-2)
当x>
|
| ||
| 3 |
由对称性画出草图n∈[a-1,a+1]
∵1<
2
| ||
| 3 |
∴m∈[a-1,a+1],f(n)为n∈[a-1,a+1]时的值域的长度d.要使f(n)的值域最小当a-1<-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| 8 |
| 9 |
| 6 |
| 16 |
| 9 |
| 6 |
故答案为
| 16 |
| 9 |
| 6 |
点评:本题求解的关键是利用具体函数,研究出函数所具有的性质,进而研究面积S的最小值

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|