题目内容
(Ⅰ)求极坐标方程ρsin2θ-2•cosθ=0表示的曲线的焦点坐标;
(Ⅱ)设直线l:
(t为参数)与题(Ⅰ)中的曲线交于A、B两点,若P(2,3),求|PA|•|PB|的值.
(Ⅱ)设直线l:
|
(1)解(1)由ρ•ρsin2θ-ρ•2•cosθ=0
得y2=2x------------(4分)
焦点(
,0)------------(6分)
(2)设A,B两点对应的参数分别为t1,t2,
将
代入y2=2x------------(9分)
得
t2+
t+5=0------------(11分)
∴t1t2=
即|PA|•|PB|=|t1t2|=
------------(14分)
得y2=2x------------(4分)
焦点(
| 1 |
| 2 |
(2)设A,B两点对应的参数分别为t1,t2,
将
|
得
| 16 |
| 25 |
| 18 |
| 5 |
∴t1t2=
| 125 |
| 16 |
即|PA|•|PB|=|t1t2|=
| 125 |
| 16 |

练习册系列答案
相关题目
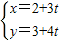 (t为参数)与题(Ⅰ)中的曲线交于A、B两点,若P(2,3),求|PA|•|PB|的值.
(t为参数)与题(Ⅰ)中的曲线交于A、B两点,若P(2,3),求|PA|•|PB|的值.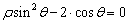 表示的曲线的焦点坐标;
表示的曲线的焦点坐标;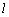 :
: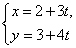 (
(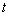 为参数)与题(Ⅰ)中的曲线交于A、B两点,若P(2,3),
为参数)与题(Ⅰ)中的曲线交于A、B两点,若P(2,3),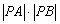 的值.
的值.