题目内容
(1)以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线的极坐标方程为θ=
(ρ∈R),它与曲线
(θ为参数)相交于两点A和B,求|AB|.
(2)在直角坐标系xOy中,直线L的参数方程为
(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4cosθ.设圆C与直线L交于点A、B.若点P的坐标为(3,-2),求|PA|+|PB|及|PA|•|PB|.
| π |
| 4 |
|
(2)在直角坐标系xOy中,直线L的参数方程为
|
分析:(1)先利用直角坐标与极坐标间的关系,将极坐标方程为化成直角坐标方程,再将曲线C的参数方程化成普通方程,最后利用直角坐标方程的形式,利用垂径定理及勾股定理,由圆的半径r及圆心到直线的距离d,即可求出|AB|的长.
(2)先根据题意得出圆C的普通方程,再根据直线与交与交于A,B两点,可以把直线与曲线联立方程,用根与系数关系结合直线参数方程的几何意义,求出答案.
(2)先根据题意得出圆C的普通方程,再根据直线与交与交于A,B两点,可以把直线与曲线联立方程,用根与系数关系结合直线参数方程的几何意义,求出答案.
解答:解:(1)∵ρ=
,
利用ρcosθ=x,ρsinθ=y,进行化简,
∴x-y=0,
相消去θ可得
圆的方程(x-2)2+(y-1)2=5得到圆心(2,1),半径r=
,
所以圆心(2,1)到直线的距离d=
=
,
所以|AB|=2
=3
∴线段AB的长为 3
.
(2)圆C的普通方程是(x-2)2+y2=4,
将直线l的参数方程代入并化简得t2-2
t+1=0,
由直线参数方程的几何意义得,|PA|+|PB|=2
,|PA|•|PB|=1.
| π |
| 4 |
利用ρcosθ=x,ρsinθ=y,进行化简,
∴x-y=0,
|
圆的方程(x-2)2+(y-1)2=5得到圆心(2,1),半径r=
| 5 |
所以圆心(2,1)到直线的距离d=
| 1 | ||
|
| ||
| 2 |
所以|AB|=2
| r2-d2 |
| 2 |
∴线段AB的长为 3
| 2 |
(2)圆C的普通方程是(x-2)2+y2=4,
将直线l的参数方程代入并化简得t2-2
| 5 |
由直线参数方程的几何意义得,|PA|+|PB|=2
| 5 |
点评:(1)本小题主要考查圆的参数方程和直线的极坐标方程与直角坐标方程的互化,以及利用圆的几何性质计算圆心到直线的距等基本方法,属于基础题.
(2)此题主要考查参数方程的优越性,及直线与曲线相交的问题,在此类问题中一般可用联立方程式后用韦达定理求解即可,属于综合性试题.
(2)此题主要考查参数方程的优越性,及直线与曲线相交的问题,在此类问题中一般可用联立方程式后用韦达定理求解即可,属于综合性试题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
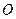 为极点,
为极点,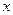 轴的正
轴的正 半轴为极
半轴为极 轴。已知点
轴。已知点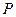 的直角坐标为(1,-5),点
的直角坐标为(1,-5),点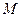 的极坐标为
的极坐标为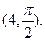 若直线
若直线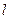 过点
过点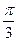 ,圆
,圆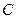 以
以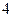 为半径。(I)求直线
为半径。(I)求直线 先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于
先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于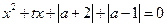 对任意
对任意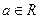 无实根,求实数
无实根,求实数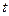 的取值范围.
的取值范围.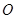 为极点,
为极点,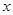 轴的正
轴的正 半轴为极
半轴为极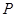 的直角坐标为(1,-5),点
的直角坐标为(1,-5),点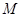 的极坐标为
的极坐标为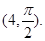 若直线
若直线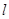 过点
过点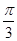 ,圆
,圆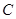 以
以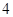 为半径。(I)求直线
为半径。(I)求直线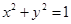 先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于
先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于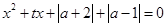 对任意
对任意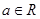 无实根,求实数
无实根,求实数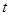 的取值范围.
的取值范围.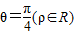 ,它与曲线
,它与曲线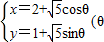 为参数)相交于两点A和B,求|AB|.
为参数)相交于两点A和B,求|AB|.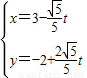 (t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4cosθ.设圆C与直线L交于点A、B.若点P的坐标为(3,-2),求|PA|+|PB|及|PA|•|PB|.
(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4cosθ.设圆C与直线L交于点A、B.若点P的坐标为(3,-2),求|PA|+|PB|及|PA|•|PB|.